
Figure 1: US Replica of a Purple Cipher
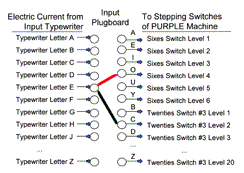
Figure 2: Plugboard of a Purple Cipher
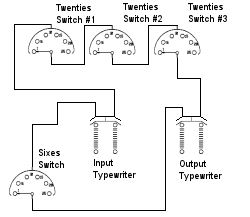
Figure 3: Schematic of a Purple Cipher
The plugboard had plugs for every letter of the Roman alphabet. The machine would super-encipher alphabets, ie repeatedly encipher the text with many variations, making millions of cipher alphabets available for substitution.
Inside the machine, letters were divided into two groups. The first group consisted of the vowels, AEIOUY, and were known as the “sixes”. The second group, the “twenties” corresponded to the rest of the alphabet.
Any input from the electric typewriter could be plugged into any input of the PURPLE machine. For example, if typewriter letter 'E' was plugged into input 'O' then it would be enciphered as one of the sixes. If 'E' was plugged to 'C,' however, it was enciphered as one of the twenties. (See Figure 2.)
The sixes letters were enciphered on a single 6-level, 25-position stepping switch. Each position of the sixes switch produces a new random alphabet. The sixes switch advances each time a letter is enciphered, however, so the sixes alphabets will repeat every 25 letters.
The twenties letters are enciphered on three cascaded stepping switches. Only one of the twenties switches advances with each enciphered letter, so the twenties alphabets will not repeat until 15,625 letters have been enciphered. Any of the twenties switches can be the 'fast,' 'medium,' or 'slow' stepping switch, which means that there are six possible switch motions. (See Figure 3.)
Furthermore, this type of encryption meant that there was no logical way of predicting what a letter typed on the first typewriter might end up on the second typewriter. As a result, frequency analysis could not be used.
Purple relied on five-digit groups. It allowed 45,000 entries in both an alphabetic encoding dictionary and a numerical encoding dictionary. The numerical encoding dictionary scrambled the alphabetic code, thereby making it harder to decipher.
However, that was the not the end of the code. The Japanese “falsely added” an arbitrary five-digit number segment, called an additive, from a separate codebook to each pre-encoded five digit group.
In “false addition”, if two numbers add and the result is greater than 10, only the 1’s digit is used. For example, 68238 + 32490 = 90628 rather than the traditional result of 100728. A similar process is used for “false subtraction” in the decryption process.
All additive five-digit segments were made divisible by three which lead to an attenuated form of garble or corruption checking. If the received code was not divisible by three, it was thrown away.
In all, there were 18,000 additives in the enciphering book. That meant that there were 45,000 potential code groups that could each be encoded 18,000 different ways. That is 810 million different possibilities.
The system seemed unbreakable, since one needed the additives in order to figure out the basic code-groups, but needed the basic code-groups to find the additives. One needed to subtract that additive then undergo repeated analysis of the remaining usage patterns in an effort to determine the meaning of the original five-digit group. All of this had to be done without the aid of modern computers.