
Breaking Enigma
In defiance of the Versailles Treaty of 1919, Germany was strengthening her military forces from year to year. Abroad, intelligence operations were being conducted by Germany's numerous intelligence offices, where the military was disguised as Abwehr, [or military intelligence], espionage - near the borders with Poland and Czechoslovakia. Germany had also commissioned a radio intelligence organization that employed many monitoring personnel and decryptment specialists. Unfortunately, little is known about the first phase in the Polish-German cryptological duel, which all started immediately following World War I, as well as the reemergence of Poland as an independent state.
In the middle 1920s, German radio intelligence started reading messages between the staffs of the Polish Air Force. Accurate information was gained about locations of most of the units. Poland's Section II (military intelligence) had noticed a setback; for some period of time, the instructions for German agent in Poland hardly carried any assignments concerning air force units, whereas the Polish Air Force and air defenses had been really interesting to German intelligence. This all suggested that information was leaking somehow, and assignments had to be shifted. The Polish decided to dole out some false information in this same fashion to throw the Germans off course, while still communicating with themselves through courier and coded telephone messages. The Abwehr never detected this code, entitled "Port," and this more or less neutralized the damage the Germans had previously caused.
In the later half of 1932, Polish-German relations were exceptionally strained. For many years Germany had been waging tariff and economic war against Poland. Radio monitoring allowed for Poland to learn of Germany's diplomatic and military plans, provided that there were ways developed for solving German codes and ciphers. This was becoming harder all the time, though, because Germany was increasingly using machine ciphers. Every so often, the Germans tried to make things a little more difficult. They altered from alphabetical order, to leaving out letters of the alphabet, to even broadcasting bogus code groupings.
The earliest Polish work on the German machine cipher
had begun in 1927-1928, a short while after the system had been introduced
by the German Navy and Army. Germany's armed forces faced the dilemma of
"reconciling the requirements of security with the imperatives of speed
and convenience" [Kozaczuk]. Since 1918 the German Navy had been contemplating
the use of cipher machines. Many designs were considered, but there was
one developed by Dr. Arthur Scherbius, that became very powerful. The name
of the machine was the "Enigma." This machine was then patented. Attempts
had been made to solve Enigma by resorting to leading mathematicians and
to parapsychology.
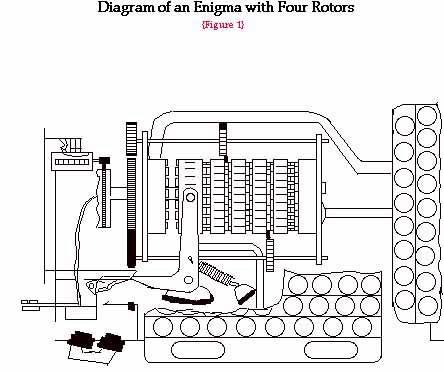
On the outside, the machine resembled a typewriter, with an extra panel built into the lid. There were twenty-six little circular glass windows in the panel, which bared the letters of the alphabet, just like the keyboard. On the underside of the panel were a corresponding number of glowlamps. Inside the machine there was originally a set of three rotors, otherwise known as rotating drums, and a "reversing drum" all mounted on one axle. An intricate system of wiring included this axle. Powering this machine was done by a battery or a regular current which passed through a small transformer.
When a key was pressed, one or more of the rotors revolved. Concurrently, a glowlamp beneath the panel lit up, illuminating the letter in the window above it. The design of the Enigma machine allowed the user to "type" the plain text while the letters of the cipher text lit in the appropriate windows and, conversely, when one "typed" out a cipher text, the letter illumination spelled out the plain text. The secret dialog was only conducted through both parties having the identical devices set, using various knobs and levers, to the same cipher key. Although the commercial Enigma gave general insight to the machine's construction and operation, the military version had completely different wiring and additional components.
It all began in ancient Greece. The roots of cryptography and cryptology began to grow. The history of this field contains names such as Julius Caesar, who invented "Caesar ciphers." These codes deal with the shifting of letters to a specific key letter. Another famous name is Blaise de Vigenere, where his coding system revolves around a table of all the two-letter combinations of the alphabet. Thomas Jefferson invented the "wheel cypher." Edgar Allen Poe demonstrated that any substitution cipher can be solved given long enough cipher text. In the computer world, we have Charles Babbage who first attempted to apply algebra to the solution of ciphers. A noted linguist named August Kerckhoffs codified knowledge about ciphers and determined that the variability of the key determines the strength of the cipher rather than the physical security of the device. "Cryptography and cryptology have developed in parallel with the evolution of science and technology" [Kozaczuk].
The cryptologists would need to continue studying the Enigma system from the mathematical side in order to break the code. Group theory, one of the divisions of higher mathematics, and the properties of permutation groups would be very useful tools in studying the military Enigma.
Since 1927, the Polish Cipher Bureau had been working on the Enigma cipher. Other than intercepts, there was nothing else that the Polish had to go on, so any new information was welcome. France and Czechoslovakia, like Poland, were threatened by German expansionism. They were also allies for Poland in collecting intelligence on German armaments and plans for war. Even though France and Poland had their disagreements since their alliance in February of 1921, cooperation among their intelligence services was very important.
In December of 1932, tasks were established between the nations. The French were to put their concentration towards furnishing intelligence from Germany which might facilitate the breaking of the machine cipher, while the Poles worked with theoretical studies of Enigma intercepts. German radio intercepts were to be exchanged while radiogonometric data was to be studied. Other intelligence was also to be worked with during the procedures. The Warsaw Cipher Bureau was also hiring mathematicians who were experienced with German ciphers. "The principle of strict secrecy and compartmentalization meant that even the most trusted radio intelligence and encryptment workers learned only as much as was indispensable to their own work about the materials supplied to them" [Kozaczuk]. The brains of the German Cipher office, the three mathematician- cryptologists the Polish had, had no knowledge of the Polish-French contacts or of the origin of the information which was supplied to them on the Enigma.
One Polish cryptologist by the name of Marian Rejewski
received documents concerning the machine's operation, key instructions
and obsolete tables of daily keys. Rejewski discovered that in the commercial
Enigma the letters of the alphabet were represented on the circumference
of the entry ring in the same order which they appeared on a German typewriter
keyboard. He then wondered what the order would have to do with the military
Enigma. Since both keyboards are ordered the same way, Rejewski assumed
that the entry ring was set up in the same manner. After lots of research,
he determined that since the keyboard wasn't wired to the entry drum in
keyboard sequence that maybe the wiring was in alphabetical order. By testing
this hypothesis in the manner of designating connections in a specific
rotor, he realized that the right-hand rotor turned one twenty-sixth of
a revolution each time a key was depressed.
February 1933 began a period of "Enigma-doubling." Duplicates were being made of the military version of the Enigma. By 1934, over a dozen of these machines existed. To recover the settings, or starting positions, and the keys, the process of elimination was put into play. The connections in the commutator would be found by using the grill method. There were a possibility of 100,391,791,500 different connections. The rotors had to be turned as many as 17,576 ways to find the keys. There were 263 possible settings for each of the six possible sequences of the three rotors. This was a time-consuming job for the mathematicians, and, "in their haste, the men would scrape their fingers raw and bloody" [Kozaczuk]. The Germans, being as sly as they could be, began changing the commutator connections infrequently, once a quarter, at first. But, in 1934, they started changing them monthly, and after a while, daily, and to make matters even worse, they started changing the connections every eight hours!
Rejewski then invented what he called the cyclometer. This was a device that determined the length and number of cycles in the "characteristic" for each position of Enigma's rotors. The cyclometer enabled the mathematicians to set up a catalog of characteristics which could encompass the 105,456, or 6 x 263 possible settings of the rotors. The cyclometer also had the ability to "annihilate" the connections in the commutator, which constituted one of Enigma's stronger points.
In November and December of 1932, the most intensive work had been in progress on Enigma in Poland. German cipher clerks were committing crazy blunders to try to get the Poles off their track. They would send the same letter three times (AAA) or they would punch the letters in alphabetical order (ABC). The Germans would also type in letters which were in a diagonal line across the keyboard, which was also against regulations. "Perhaps the cipher personnel were still imperfectly trained and the supervision by their bosses superficial" [Kozaczuk]. There is a crux of the matter, though, - blind faith in the Enigma, a belief that it could take any message and transform it into an unbreakable cipher text. With some mathematical analysis, Rejewski was able to reduce the number of unknowns in equations for solving Enigma codes. So, nothing is unbreakable; with enough work, anything can be solved.
In February of 1936, there was a special "A" key which was introduced into secret correspondence. This is the reflector, or reversing drum. In 1937, though, the Germans exchanged this reflector to introduce a new "B" key. But, the Germans made a mistake; they forgot to change the wiring in the three rotors at the same time. Because this change was not as effective as the Germans anticipated, Enigma signals continued to be read in Poland.
In September 1938, the Germans completely altered
the rules used by Hitler's army, navy, air force, and key civil agencies.
Rule alterations allowed for , the Enigma operator, on his own, to select
the basic position, a different one each time, for enciphering the individual
message key. But because the old keying procedures were being used, the
Polish cryptologists continued to read the trickle of information.
The bomb was an electro-mechanical aggregate based on six Polish Enigmas. Six of them were constructed at once. They were combined with additional devices and transmissions. The bomb was composed of electronically driven rotors which revolved automatically, creating in each bomb, successively, 17,576 different combinations. As the rotors aligned in the aimed-for position, a light went on, automatically the motors stopped, and the combinations were read by the cryptologist. When the bombs were set in motion, the daily keys could be recovered in two hours. Axle shafts, transmission wheels, and special instantaneous glowlamps were some of the same ideas that constituted some of the existing technology from the Enigma. About the same time the bomb came about, there was a method which was discovered for breaking the doubly enciphered individual message keys to be used in accordance with the new procedures the Germans set forth in September 1938. This new method consisted of a series of perforated sheets of paper with the capacity of fifty-one holes by fifty-one. Each series consisted of twenty-six sheets. Designed mainly by Henryk Zygalski, the third mathematician, this system was effective in matching the coincident places in this preprogrammed system. It did not matter how many plug connections there were in the German Enigma's commutator.
Using the bombs and the perforated sheets, the cryptologists were once again able to find keys to the signals. As soon as the key was broken, cipher clerks set sometimes more than a dozen Enigma doubles into operation, turning the columns into readable plain text.
In December 1938, another big change erupted. The Germans once again revamped their Enigma ciphers. This time the change involved more than just changing procedures. It involved changing the components as well. The Germans introduced two additional rotors per device, making the number of rotors five instead of three. Even though only three rotors could be operated in any one machine at one time, the sequence that they were used could be altered. Five rotors were selected from, which made many more combinations possible. This, once again, nullified the Poles' chances of decrypment by the methods so far used. But, by mathematical and other operations during the second half of December and the first few days of January 1939, the internal connections in rotors four and five were reconstructed. The Poles were again on top of things and the cryptologists had no secrets held from them. The possibilities of again reading the correspondence of the German land and air forces opened up. Nevertheless, even though the bomb and the perforated sheets were being used, the new keying procedure and the increased number of rotors posed major problems. To make matters even worse, the Germans then increased the number of plug connections in the commutator.
So, even though the Poles continued to read the Germans'
codes without great difficulty, with all the complications added, the continuous
decrypment would have required the investment of ever greater resources.
Many cryptological bombs were in use; at least sixty were known to be existant.
Everything was getting very expensive for the Polish, as they had to train
many new skilled workers, keep up with the modern equipment, secure teletype
lines for direct transmittal of intercepts, and increase the number of
monitoring stations. Large numbers of Polish Enigmas were necessary, because
they constantly wore out from the overuse. "The solution of the Enigma
cipher just as Hitler was taking power had secured a regular flow of reliable
military, political, and other information from Germany" [Kozaczuk].
Time passed, and the war continued. In 1941, a cipher was solved that turned out to serve communication between German secret agents. The cipher was broken by an engineer, who, while maintaining the Enigma ciphers and radios, restored his old cryptological specialty. These reconstructed spy reports were sent to France where the Rural Works Enterprise discovered the transmitter and neutralized the agents. At a later time, Rejewski, Rozycki, and Zygalski broke codes and ciphers used in German telegraphic communications. French postal workers cooperating with the Germans took the encrypted texts and copied them. Included were reports from German radio-location and monitoring stations in southern France that were used to find the secret transmitters of undergorund organizations.
The mathematicians' knowledge of the adversary increased
from knowledge of other German codes. The decryption of German messages
helped them discover the newly introduced principles of preliminary preparation
of texts and make tables of standard abbreviations, signals, and others.
In the middle of 1941, they determined that the Germans were enciphering
numbers as well, and they were varying the endings. This created more possibilities
of combinations which made decryption more difficult. The Germans had other
precautions as well. It was against the law to resend a message which had
errors in it the first time. The text had to be reedited without changing
the content. Usually, the order of the expressions would be changed.
"Part One: The Machine": The Enigma cipher machine could be operated in a variety of ways. The rotors were set in the basic position. Each message had its independently selected key where three letters were enciphered twice. This way, six letters were obtained. Encipherment began from the same position in the message, which was unknown to the cryptologist. The rotors were then set to a selected individual key. Each key was enciphered twice. If there is a sufficient number of messages in a given day, then all the letters in the alphabet will occur in all six places at the openings of the messages. Permutations are formed, thus constituting the starting point for solving Enigma. These permutations, designated respectively by the letters A through F, form products AD, BE, and CF because the transitions by the rotors change letters from the first letter to the fourth letter, from the second letter to the fifth letter, and from the third letter to the sixth letter. This is using a specific permutaion. "They may be represented as disjunctive products of cycles and then assume a very characteristic form, generally different for each day, for example:
AD = (dvpfkxgzyo) (eijmunqlht) (bc) (rw) (a) (s)
BE = (blfqveoum) (hjpswizrn) (axt) (cgy) (d) (k)
CF = (abviktjgfcqny) (duzrehlxwpsmo)."
Using these sets from days worth of retrieving messages, the mathematicians managed to reconstruct the machine's internal connections. According to Rejewski, we know from the machine's description that, if striking a given key "x" causes the "y" lamp to light, then, conversely, striking the "y" key will cause the "x" lamp to light. For example, if the encipherer continues striking keys, and first he strikes the unknown key "x" and obtains the letter "a", and in the fourth letter place, he again strikes the same unknown letter "x" and this time, obtains a "b," then by striking the "a" key in the first place, he would obtain the letter "x," and in the fourth place if he struck the "b" key, he would obtain the letter "x" as well. There is a successive action occurring - first of "a" on "x," and then of "x" on "b." So, when "ab" are written next to each other, a fragment permutaion of AD is written, which is a product of the unknown permutations A and D.
"Let us now consider the following example. Let
dmq vbn
von puy
puc fmq
designate the openings, that is, the double enciphered keys, of three of some eighty messages available for a given day." Looking at the first and fourth letters, notice that "d" becomes "v," "v" becomes "p," "p" becomes "f." A fraction of the permutation AD, "dvpf" is obtained. Noticing the second the second and fifth letters, "o" becomes "u," "u" becomes "m," "m" becomes "b." A fragment of BE, "oumb" is now obtained. Lastly, from the third and sixth letters, "c" becomes "q," "q" becomes "n," "n" becomes "y." "cqny," a fragment of CF is also arrived at. "The openings of further messages would permit a complete assembly of the set of permutations AD, BE, CF. Because of its configuration and fundamental importance, we shall call this set the characteristic set, or, simply, the characteristic for the given day."
After a key has been depressed and before the current causes a given lamp to light, it starts passing through a series of the machine's components. Each component causes a permutation of the alphabet.
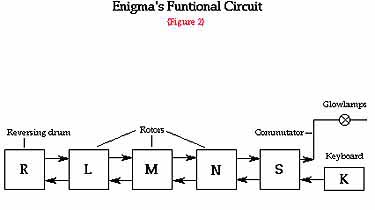
"If we designate the permutation caused by the commutator with the letter S, and that which is caused by the three rotors respectively (from left to right) with the letters L,M,N and that which is caused by the reversing drum with the letter R, then the path of the current will be represented by the product of permutations SNMLRL-1 M-1N-1S-1" [Rejewski]. When the key is pressed, the rotor N turns one twenty-sixth of a revolution, and Rejewski introduces a special permutation to name this cycle that transforms each letter of the alphabet into the next one. He designates it with the letter P:
P = (a b c d e f g h i j k l m n o p q r s t u v w x y z).
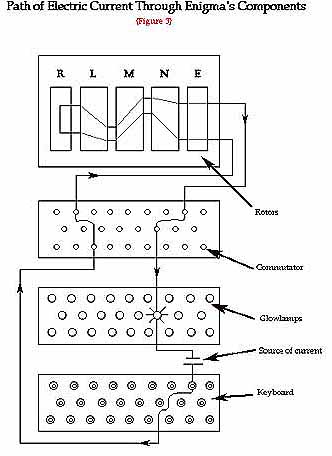
In the diagram, the current before and after the movement of rotor N is shown. Rejewski explains that the equations,
A = SPNP-1MLRL-1M-1PN-1P-1S-1
B = SP2NP-2MLRL-1M-1P2N-1P-2S-1
.................................................
E = SP5NP-5MLRL-1M-1P5N-1P-5S-1
F = SP6NP-6MLRL-1M-1P6N-1P-6S-1
make up the known products AD, BE, CF, which are expressed in the form:
AD = SPNP-1MLRL-1M-1PN-1P3NP-4MLRL-1M-1P4N-1P-4S-1
BE = SP2NP-2MLRL-1M-1P2N-1P3NP-5MLRL-1M-1P5N-1P-5S-1
CF = SP3NP-3MLRL-1M-1P3N-1P3NP-6MLRL-1M-1P6N-1P-6S-1.
The first part of the task is to solve the set of equations. On the right side only the permutation P and its powers are known. The permutations S,L,M,N,R are unknown. We now need to simplify the set. The first step consists in replacing the repeated product MLRL-1M-1, let's call this the "fictitious" reversing drum, with the single letter Q. So now the number of unknowns are namely three, S, N, Q:
AD = SPNP-1QPN-1P3NP-4QP4N-1P-4S-1
BE = SP2NP-2QP2N-1P3NP-5QP5N-1P-5S-1
CF = SP3NP-3QP3N-1P3NP-6QP6N-1P-6S-1.
Rejewski also continues to explain the next step, which includes the Theorem on the Product of Transpositions. From the now known products AD, BE, CF we need to now determine separately the permutations A through F. The permutations consist only of transpositions, and AD, BE, CF are their products. Applying them to the following theorem: If two permutations of the same degree consist solely of disjunctive transpositions, then their product will include disjunctive cycles of the same lengths in even numbers, gets us to Rejewski's proof of the theorem.
"Proof: As an example, we designate the permutations to be multiplied by each other by the letters X and Y, and their degree by 2n. If, in permutation X, there happens to occur a transposition identical with a transposition occurring in permutation Y, for example (ab), then, in the product XY, there will occur a pair of uniliteral cycles (a) (b). With reference to transpositions identical in both permutations the theorem is, therefore, true. After rejecting these identical transpositions, we may without prejudice to generality assume that
in permutation X in permutation Y
there will occur there will occur
the transposition the transposition
(a1a2) (a2a3)
(a3a4) (a4a5)
..................... .....................
(a2k-3a2k-2) (a2k-2a2k-1)
(a2k-1a2k) (a2ka1)
because the initial letter a1 must finally occur in permutation Y. When we proceed to execute the multiplication XY, obviously we shall always obtain two cycles of the same length k ¾ n:
(a1a3.....a2k-3a2k-1) (a2ka2k-2.....a2ka1)."
Not all the letters have been exhausted in this method, but the procedure is continued until they have all been found. Rejewski notes that the letters which are in the same transposition are always involved with two different cycles of the same length, of permutation XY. He also states that if two letters occur in two different cycles, of the same length, of permutation XY, which also happen to belong to the same transposition, then the letters adjacent to them also belong to a single transposition. The converse theorem states: If a permutation of even-numbered degree includes disjunctive cycles of the same lengths in even numbers, then this permutation may be regarded as a product of two permutations, each consisting solely of disjunctive transpositions.
A proof is unnecessary for this converse theorem to give a formula for the number of possible solutions for X and Y. When this theorem is applied to the products AD, BE, CF, supplies for each of the expressions A,B,C, whereas permutations D,E,F are determined uniquely by the former. There are several thousands of different possible solutions for the whole characteristic set of three equations. If we were to extract the one true solution out of the many that exist, it would be very difficult. This theorem did not bring us to the goal we want, but it did bring us closer. If we had some knowledge of the keys for the messages, or some other knowledge of the encipherers' habits, plus the theorem on the product of transpositions, this now enables us to find the one correct solution, so that in the set of equations
A = SPNP-1QPN-1P-1S-1
B = SP2NP-2QP2N-1P-2S-1
...................................
F = SP6NP-6QP6N-1P-6S-1,
we may label the left sides as known. But, most often, before breaking the cipher, the cryptologist does not usually know the encipherers' habits.
"Whether the foregoing set of six permutational equations with three unknowns S, N, Q is soluble without further supplementary data is not known to this day. However, it is known that this set would be soluble if the cryptologist had cipher material for two different days, with different plug connections, but with the same or nearly the same setting of rotors." The number of possible settings of the rotors is 6 (26) (26) (26) = 105,456. In a number of days, let us say five hundred, the same setting of the rotors may appear twice. But, the goal is still tough to reach, because we would have to go through all the other days as well. In theory, though, it is still soluble. In reality, though, the necessary supplementary data were obtained by a much shorter way.
The French Cipher Bureau supplied the Polish Cipher Bureau with intelligence material containing German tables of Enigma keys, which also included the S commutator connections, in December 1932. The S permutation became possible to be transferred, as a known, to the left side of our set:
S-1AS = PNP-1QPN-1P-1
S-1BS = P2NP-2QPN-1P-2
..................................
S-1ES = P5NP-5QPN-1P-5
S-1FS = P6NP-6QPN-1P-6
having six equations with only two unknowns, N and Q. "This set is now soluble, but for various reasons, mainly in order to make certain whether within the six permutations A through F there does not occur a movement of rotor M, it is advisable to carry out certain transformations."
Transforming both sides of the first equation by P, of the second equation by P2, and so on, to simplify things, we denote the left sides by the letters U through Z:
U = P-1S-1ASP = NP-1QPN-1
V = P-2S-1BSP2 = NP-2QP2N-1
.........................................
Y = P-5S-1ESP5 = NP-5QP5N-1
Z = P-6S-1FSP6 = NP-6QP6N-1.
Two products of each two successive expressions are formed:
UV = NP-1 (QP-1QP) PN-1
VW = NP-2 (QP-1QP) P2N-1
WX = NP-3 (QP-1QP) P3N-1
XY = NP-4 (QP-1QP) P4N-1
YZ = NP-5 (QP-1QP) P5N-1.
By eliminating the common expression QP-1QP, a set of four equations with only one unknown NPN-1 is obtained:
VW = NP-1N-1 (UV) NPN-1
WX = NP-1N-1 (VW) NPN-1
XY = NP-1N-1 (WX) NPN-1
YZ = NP-1N-1 (XY) NPN-1.
Continuing using this method, from the first equation,
NPN-1, there are several dozen expressions arrived at, depending on the
permutation of UV. The same number of solutions will be obtained for NPN-1
from the second equation, and one of these solutions must be identical
with one solution for the first equation. The final two equations are now
superfluous. We will need to apply the indicated method once again by comparing
the solution obtained for NPN-1 with permutation P. "We will obtain twenty-six
possible solutions for N-1 that do not differ essentially, and, after selecting
one of them, we will readily obtain N itself, the internal connections
of the right-hand rotor."
"Part Two: Keys": Methods had to be devised for rapid reconstruction of the daily keys in order to solve codes. The permutation theory will help explain, how, once having the machine, one can reconstruct the keys. "As the formulas for AD, BE, CF show, permutation S, as a transforming permutation, influences solely the letters within cycles comprising permutations AD, BE, CF, but does not influence the actual configuration of these cycles." There are three rotors which can be placed on an axis in six different ways. The rotors can take on (26) (26) (26) = 17,576 different positions, as described earlier. If a machine existed, which could give the length and number of cycles, and if these figures were catalogued, then the products AD, BE, CF could be compared for a given day with products of the same configuration. Such a devise was designed, and its name was the cyclometer.
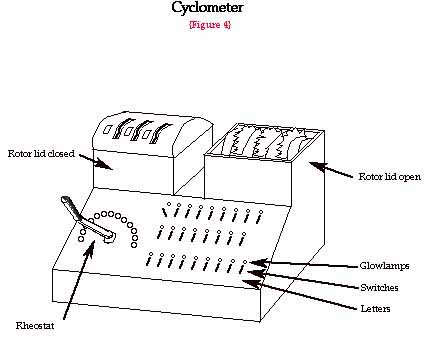
The main part of the cyclometer comprised two sets of rotors suitably connected by wires through which electric current could run. The device would turn the rotors one by one while counting the lamps that light. From this information, one can determine the length and number of cycles. Since there were six possible sequences, the catalog of characteristics enveloped a total of (6) (17,576) = 105, 456 entries.
Beginning on September 15, 1938, the catalog of characteristics based on the cyclometer no longer fulfilled its task. The Germans instilled completely new rules for enciphering message keys. Hence, the Enigma operator himself was the one who selected the basic position, a new one each time, for enciphering the individual message key. The key, as before, was enciphered twice. The first letter continued to designate the same thing as the fourth letter, the second the same as the fifth, and do on. The basic position was now known to the cryptologist, but unfortunately was different for each message. Therefore, there were no products AD, BE, CF characteristics daily, whose configuration could be found in the catalog. "Since the length of the cycles in products AD, BE, CF was invariable with respect to the transformations produced by permutation S, the occurrence or nonoccurrence of constant points in the products was invariable with respect to those transformations."
A catalog of constant points for all the 17,576 possible products was now needed. If the constant points, which occurred in the catalog about forty percent of the time, were transferred to a long tape, they would have formed a distinct pattern. Then from this first tape, if transferred to a second tape according to the positions of the constant points, the task would be to determine where it collided with the constant points on this second tape. Since this was a very difficult method, Henryk Zygalski came up with the idea of perforated sheets, letters "a" through "z."

This was a system of coordinates in which the abscisses and ordinates marked successive possible positions of rotors. Cases with constant points were perforated. According to the diagram, we can see that each constant point had to be perforated as many as four times. The sheets were superimposed and moved with respect to each other, in accordance with a strictly defined program, so the number of visible apertures gradually decreased. If the sufficient quantity of data was available, then there remained a single aperture, probably corresponding to the solution. Once the position of the aperture was determined, one could calculate the order of the rotors, the settings of their rings, and by comparing the cipher letters with the machine letters, (otherwise known as permutation S,) one could in other words calculate the entire cipher key.
The German cipher service constantly introduced difficulties designed to frustrate those trying to recover the keys. These ploys had to be dealt with. In November 1937, the reversing drum was exchanged. The number of connections in the commutator was gradually increased form six to thirteen pairs. In December 1938, the number of rotors was increased from three to five. German radio communications nets grew from year to year. Even though they used the same Enigma devices, different keys were used. By September 1939, almost all the Cipher Bureau's equipment and most of its records were destroyed due to the evacuation. But, in July of 1939, the Polish, the French, and the British cipher bureau representatives met and decided to make available all its devices and methods for Enigma decryptment to future war allies. They also agreed to hand over a copy of the German Enigma cipher machine that had been reconstructed in Poland on the basis of the theoretical work that was described in "The Mathematical Solution of the Enigma Cipher," by Marian Rejewski.
Kozaczuk, Wladyslaw. Enigma: How the German Machine Cipher Was Broken, and How It Was Read by the Allies in World War Two. Washington D.C.: Library of Congress Cataloging Publication Data. 1984
Other links of interest to the Enigma
Story:
The Enigma Cipher- http://www.trincoll.edu/~cpsc/cryptography/enigma.html
Alan Turing: The Enigma- http://www.wadham.ox.ac.uk/~ahodges/book.html
The Enigma by Jason Chapman- http://shakti.trincoll.edu/~rmorelli/FYSM122/docs/chappy.html
Honors Seminar in Cryptography. Spring Semester, 1997
University of Illinois at Chicago- http://raphael.math.uic.edu/~jeremy/crypt/crypt.html
enigma/concepts- http://www.enigma.com/eci.machine.1.html
An Enigma Machine Written in Basic- http://www.unix-ag.uni-kl.de/~conrad/krypto/misc/enigma.bas