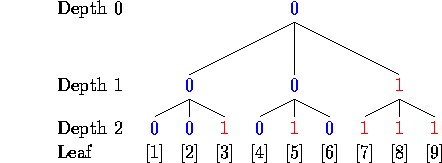

We want to find the value assigned to the root. An upper bound on the number of leaves that we have to examine to compute this is 3d (that is, all of them). However, if we are lucky, we may be able to examine fewer: if in any group of three sibling nodes, the first two examined have the same value, that value propagates up to the parent, and there is no need to look at the third node or any of its descendants; they are rendered irrelevant.
For example, in the tree shown above, if we read the leaves from left to right, skipping irrelevant ones, then we would first examine leaf [1]
and leaf [2]
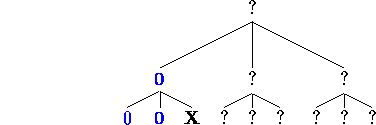
In their group of siblings [1-3], they give two 0's, so there is
no need to examine leaf [3]; we just propagate the value 0 up a level,
and mark [3] as "irrelevant" with an "X."
Then we examine leaf [4]
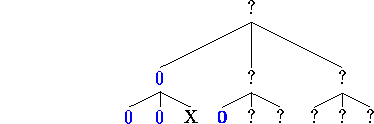
and leaf [5]
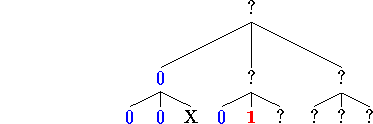
and still do not have a majority in the sibling group [4-6]. We read leaf [6]

and the majority value of leaves [4-6] is 0, so we set their parent
to 0. This makes two of the siblings on level 1 have value 0, so
the root has value 0 too; there is no need to examine the third
node on level 1, or its children [7-9], so mark them irrelevant.
Examining the leaves in this order required seeing the values of 5 leaves.
If instead of reading the leaves left to right, we chose the order by some other rule, and we happened to start out [1] [2] [4] [6], we would know the value of the root is 0 after examining just 4 leaves.
We can turn this into a 2-player (mathematical) game. For each round of play,
Then play another round. Eventually, the value of the root will be determined.
The applet below demonstrates this game.
Here are some questions about how many leaves the solver must examine. See the problem set and solutions.
The applet below has several strategies for the two players:
The node values are displayed as follows:
<| |> Do one step forwards or backwards. < || > Animate the steps. << >> Clear the game, or jump to the end of the game.
If Node View is set to Counts, then the order in which the leaves are assigned 0/1 values is indicated in parentheses after the 0 or 1; if the 10th leaf given a 0/1 value is given the value 0, it is shown as "0 (10)". If this value is propagated up to ancestors, the order the ancestor nodes are assigned in is denoted "0 (10+1)", "0 (10+2)", etc. Unassigned descendants of those ancestors are marked irrelevant "X", and the order is denoted in the same sequence, "X (10+3)", etc.
0,1 The value assigned to the leaf, or calculated as the majority value of the children of a node. ? Not assigned a value yet. X The value is irrelevant because an ancestor's value could already be determined without knowing this node. The solver will not waste time choosing irrelevant leaves.
This generalizes to finite trees with all nodes having an odd number of children. The demonstration has all leaves at a specified depth, and has a specified downward degree (odd).
©2001, Glenn Tesler