Chapter 15
NCProcess: The Commands

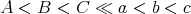
Now that the user has a feel for what we are doing we describe the NCProcess commands one runs over and over again to produce the example in Chapter 14. We are currently working on this command so it is changing with time.

15.1 SetKnowns and SetUnknowns

In most mathematics and engineering appications, certain quantities are considered known and others are considered unknown. The goal is usually to solve for unknowns in terms of the knowns, or to solve for some unknowns in terms of others. In a prestrategy session, one must declare which variables are knowns and which ones are unknowns. While this declaration evolves through the course of a session, it is, at any moment, a part of the computing environment. Indeed, before any of the NCProcess commands can be called, it is necessary to set all variables to either be known or be unknown. Mathematically, the variables which are declared unknown are those which one wants to solve for.

An example is :

After the above three commands have been executed, the user can run any of the NCProcess commands (NCProcess1, NCProcess2 or NCProcess) on any equations in the variables A, B, C, a, b, c. Here, A, B and C are knowns and a, b and c are unknowns. In the case of NCProcess and NCProcess1, setting the knowns and unknowns as above has the effect that the NCProcess command will try to solve for a, b, c and produce equations from which they have been eliminated. Also the spreadsheet displayed by the NCProcess command does bookkeeping based on what is known and unknown.

The above three commands have imposed an order on the variables A, B, C, a, b, c which expresses our priorities for eliminating them. We use the notation

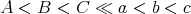
If you are running a prestrategy session and stop making progress one of the first things to try is changing the order.

The ≪ means that the NCProcess commands go to much greater lengths ¹ towards eliminating a,b,c than it does for A,B,C.

A fancier example of such prioritizing is :

This produces the ordering

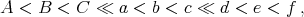
There is an alternative to SetKnowns and SetUnknowns. The command
SetMonomialOrder[{A,B,C},{a,b,c},{d,e,f}] has exactly the same effect as the commands in Example 15.2.

One can proceed with an NCProcess command, only after an ordering is set.

15.2 NCProcess

The workhorse commands of a strategy are the NCProcess1 and NCProcess2 commands. These two commands fit the general mold of the NCProcess command. In particular, each option of NCProcess is also an option of NCProcess1 and NCProcess2. See §15.6.

15.2.1 NCProcess[aListOfPolynomials,iterations,fileName, Options ]

Aliases: None

Description: NCProcess[aListOfPolynomials,iterations,fileName] finds a new generating set for the ideal generated by aListOfPolynomials along the lines of the demo presented in Chapter 16. The spreadsheets presented in §16.3.1 are the contents of the files fileName, and are produced by the command NCProcess.
In addition to creating the file fileName, NCProcess returns as Mathematica output a list consisting of three lists.

(1) A partial GB for the digested relations.

(2) The digested relations in the simplified second partial GB.

(3) The undigested relations in the simplified second partial GB.

In practice, the user runs NCProcess, then looks at the file fileName in order to get ideas for the next step. When the user decides on the next step, he can use some of the lists of Mathematica output in addition to some new relations as inputs for the next call to NCProcess. There are many options for NCProcess.

Arguments: aListOfPolynomials is a list of polynomials. iterations is a natural number. ² fileName is a character string. If fileNames’s last four characters are not “.dvi”, then “.dvi” is appended to fileName.

Comments / Limitations: Not available before NCAlgebra 1.2 If you are using NCProcess in the Windows environment you will have to quit the dvi previewer to continue your Mathematica session.

The command NCProcess calls NCMakeGB[aListOfPolynomials,iters]. NCMakeGB is an algorithm for producing a partial Gröbner basis. This produces many new relations whose solution set is the same as the solution set for aListOfPolynomials. Typically, many of the relations follow from other relations within the same output. There are many options for NCProcess which remove “mathematically redundant” relations before generating the spreadsheet in fileName and lists (2) and (3) of the Mathematica output. The various options as well as the default options for NCProcess are described in §19.

15.2.2 Examples

Here are some examples of how the NCProcess commands are called.

15.3 Commonly Used NCProcess Options and Commands

15.3.1 UserSelect → aListOfPolynomials

A valuable option for NCProcess is UserSelect. Using the option

15.3.2 DegreeCap→ aNumber1 and DegreeSumCap→ aNumber2

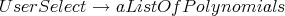
One way to reduce the run time for NCProcess is to use the options capping the degree of the polynomials that are produced in the course of running NCProcess.

This is valuable since the user will ordinarily know that a polynomial of a very high degree will not be useful to him, hence there is no reason to produce it. It is not the time that it takes to produce a large polynomial that is the primary factor; rather, it is the reduction algorithms that will get bogged down trying to remove it. Degree caps can prevent the algorithm from ever producing polynomials over a certain degree, or combining polynomials over a certain degree, and the user will still be left with a generating set for the ideal generated by the input relations. There are two different options associated with degree caps. For instance,

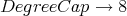
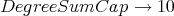
WE URGE USE OF DEGREE CAPS. THEY SAVE A LOT OF TIME.

In addition, DegreeCap and DegreeSumCap are options which cap the degree of polynomials occurring in NCMakeGB. Indeed, calling DegreeCap in NCProcess just sets the DegreeCap for running NCMakeGB inside of NCProcess.

15.3.3 MainUnknowns→ aListOfIndeterminates

If aListOfIndeterminates are given, then the output of NCProcess will only include equations whose unknowns are all contained in aListOfIndeterminates or are functions of them.

15.3.4 NCShortFormula→ Length

If NCShortFormula is set to an integer, Length, the output of NCProcess will only contain expressions whose Mathematica defined LeafCount[ ] is less than Length. This could be useful in producing TEX output when very long expressions are involved. This option also reduces run time significantly since there is much less output to process. We often have good luck with NCShortFormulas→300. If set to -1 no length elimination will be done.

WARNING The two options given above, NCShortFormula and MainUnknowns, actually eliminate polynomials from the output of NCProcess. If one of these options is set the system of equations which is the output of NCProcess is not equivalent to the system of equations which is input as is usually the case.

15.3.5 Getting Categories

GetCategory[aListOfV ariables,NCPAns] retrieves the polynomials in the category stored in NCPAns corresponding to the list of variables in the list aListOfV ariables. See Chapter 14.3. To be recognized immediately after an NCProcess run aListOfV ariables must equal a list of unknowns which corresponds to a category in that NCProcess run. The NCProcess stores all category information in NCPAns. The next NCProcess starts by clearing NCPAns and writes the category information it produces in NCPAns.

15.4 Typical use of the NCProcess command

Now we demonstrate the NCProcess command by “solving” FAC as already discussed in Chapter 14. While we show an interactive session the user probably will want to type the commands into a file and load them into your session. This is standard practice among Mathematica users and saves lots of time.

As shown in §14.2, the prestrategy starts as follows.

The first command simply loads the noncommutative Gröbner basis package into Mathematica. Then we set the variables to be noncommutative.

The third and fourth commands sets the monomial order that will be used in solving for and eliminating variables as explained in Chapter 18. The list FAC is the set of relations that describe the problem as explained in §14.2. The call to NCProcess1 will run two iterations on FAC before creating the file “Spreadsheet1.dvi” and returning the final result as Mathematica output.

The file “Spreadsheet1.dvi” is the same as the one which was produced in Chapter 16. It exists outside of Mathematica and is only for viewing. It cannot be used to create a list of polynomials for Mathematica. The strategy that the user follows at this point was described in §14.3. Recall that it led the user to select the relations

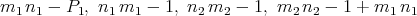
Next we describe how this is input to NCProcess1 in order to produce the second spreadsheet from §14.3.

The Mathematica output of any of the NCProcess commands is a list containing three lists. In the example above, that list is named result. Recall that in Mma the way to get sublist number j inside result is to type result[[j]].

The second round of this strategy session is

Now we discuss the input to NCProcess1 above. The variables digested and undigested hold the the last two lists from the list result which the first NCProcess1 command returned, and discovered includes the new definition of P₁. The union of these three lists is taken as the input for the second NCProcess1 run. Once again we used two iterations. This is a good number of iterations with which to start. More iterations can be used if there is a lack of progress. The next argument is a string which refers to a file name which will store the spreadsheet. Unlike the first call to NCProcess1, this call uses non-default values for the options. The UserSelect option (as described in §15.3.1) causes the discovered relations to be given high priority. The DegreeCaps are set in order to save time (as explained in §15.3.2).

The file “Spreadsheet2.dvi” is the same as the second spreadsheet which was produced in Chapter 16. As we saw in §14.4, this spreadsheet leads directly to the main theorem about factoring systems.

For another demonstration of strategies using NCProcess see Chapter 17.

15.5 Details of NCProcess

The following section gives psuedocode for the NCProcess1 and NCProcess2 commands.

This psuedocode uses the function NCMakeGB which implements a Gröbner Basis Algorithm which returns partial GB’s which are reduced. In particular, running the function NCMakeGB for 0 iterations on a set F does not compute any S-polynomials, but does produce a set G which is reduced. G will be called a reduced form of F.

15.5.1 NCProcess1 command

The input to NCProcess1 is a set of starting equations start, a number of iterations n for the GBA and a collection of user selects.

The steps NCProcess1 takes are:

I. Preparation for the main call to NCMakeGB

(1) Run the GBA on the equations in start which do not involve any unknown variables together with the user selects for at most n + 1 iterations. Let A denote this partial GB.

(2) Shrink A using the RemoveRedundantProtected operation. Call this shrunken set B.

II. The main call to NCMakeGB

(3) Run NCMakeGB with the input B together with start for at most n iterations. In this NCMakeGB run, S-polynomials between two elements of the partial GB of A are not computed. Let C denote this partial GB.

III. Shrinking the partial GB

(4) Shrink C using the RemoveRedundantProtected operation. Call this shrunken set D.

(5) Let D_k be the set of polynomials in D which do not involve any unknowns. Let D_u = D\D_k. Let E_u be a set of the normal forms of the elements of D_u with respect to D_k. Let E = D_k ∪ E_u.

(6) Let F be the union of E and the user selects. Let G be a reduced form of F (see the beginning of §15.5).

(7) Shrink G by SmallBasisByCategory using iteration parameters n + 1 and n + 2. Call this shrunken set H.

IV. Attempt Decompose

(8) Construct the collected forms of the polynomials in H.

V. Displaying the results

(9) For elements of H, if the polynomial’s only collected form is trivial, then display the rule corresponding to the polynomial, otherwise display the collected form of the polynomial. This is the step in which the “spreadsheets” of the results of this paper are constructed.

V I. Return a three tuple to the user for future use

(10) Return the triple (A,H₀,H₁) to the user where A is from item 1 above, H₀ is the set of polynomials in H which are digested and H₁ is the set of polynomials in H which are undigested.

15.5.2 NCProcess2 command

The input to NCProcess2 is a set of starting equations start, a number of iterations n for SmallBasis and a collection of user selects.

The steps taken by NCProcess2 are:

I. Shrinking the input equations

(1) Shrink start using the RemoveRedundantProtected operation. Call this shrunken set D.

(2) Let D_k be the set of polynomials in D which do not involve any unknowns. Let D_u = D\D_k. Let E_u be a set of the normal forms of the elements of D_u with respect to D_k. Let E = D_k ∪ E_u.

(3) Let F be the union of E and the user selects. Let G be a reduced form of F. (see the beginning of §15.5).

(4) Shrink G by SmallBasis. Set H equal to the result of the shrinking.

II. The “Attempt Decompose” “Displaying the results” and “Return a three tuple to the user for future use” as in §15.5.1.

15.6 NCProcess1 and NCProcess2: The technical descriptions

Below, aList is a list of polynomials, n is a positive integer, filename is a character string and rules is a sequence of zero or more Mathematica rules which correspond to NCProcess options.

For an understanding of “n,n+1,n+1,n+2”, see the footnote in §15.2 Arguments.