[next] [prev] [prev-tail] [tail] [up]

Chapter 19
More NCProcess Options

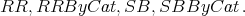
This appendix summarizes NCProcess options that were not described in Chapter 16.

19.1 Creating small generating sets: RR→ True, RRByCat→ True, SB→ False, SBByCat→ True

Section 16.3.3 discusses why the NCProcess commands used algorithms for creating small sets X from a partial GB Y such that the ideal generated by X equals the ideal generated by Y . The options of the NCProcess commands are

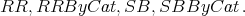
RR, RRByCat, SB, SBByCat .
These actually abbreviate longer names. For example, RR abbreviates RemoveRedundant. See §19.5. Any combination of options will leave the output of NCProcess a generating set for the ideal generated by the input relations. The more (redundant) relations you try to remove, the slower NCProcess runs. The options indicate which algorithms will be used to remove the redundant relations. RemoveRedundant, for instance, runs very quickly, but does not do a very thorough job.

A complete list of options together with indications of their speed can be found at the end of the chapter. If two overlapping options are set to True, like RR and RRByCat, then only one of them is actually run. The amount of time that it takes to run NCProcess depends on which options are set.

The defaults for NCProcess are: SBByCat and RR are set to True while SmallBasis and SBFlatOrder are set to False.

SBFlatOrder→ False

If SBFlatOrder → True the small basis algorithm will be performed under the length lexicographic monomial order. Relations which have a leading term with only one indeterminate, also known as singletons, are not included in the input to the small basis algorithm since the user typically does not want them removed. The singletons do however appear in the output of NCProcess when SBFlatOrder → True. The default is SBFlatOrder → False, however SBFlatOrder → True is probably significantly faster.

DegreeCapSB→ aNumber1 and DegreeSumCapSB→ aNumber2

Beginners should skip this part of Appendix 19 and rely on the NCProcess defaults. The reducing algorithms SmallBasis and SmallBasisByCategory call NCMakeGB (§9.3). These calls to NCMakeGB can be very time consuming and so it can be beneficial to direct NCMakeGB. The NCProcess options DegreeCapSB and DegreeSumCapSB are used when NCProcess calls SmallBasis or SmallBasisByCategory. Thus DegreeCaps are valuable in limiting the time they consume. In particular,

NCProcess[polys, iters, "filename", DegreeCapSB -> j1,  
                          DegreeSumCapSB -> j2, OtherOptions]

produces the call

NCMakeGB[polys, iters, DegreeCap -> j1, DegreeSumCap -> j2, OtherOptions]

inside SmallBasis or SmallBasisByCategory (§More appears on this in the long document describing the commands SmallBasis and SmallBasisByCategory.

The defaults at the moment inside of NCProcess are

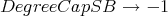
DegreeCapSB → - 1
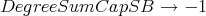
DegreeSumCapSB → - 1

19.2 NCCollectOnVars

An extremely important option for NCProcess is NCCollectOnVars. In addition to being an option, it can be called as a stand-alone command.

19.2.1 NCCollectOnVars[aListOfExpressions, aListOfVariables]

Aliases: NCCV
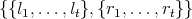
Description: This is a command which “collects” certain products of each variables in aListOfVariables, thus it returns a ”collected polynomial”. In NCProcess, when this is used via NCCV → True, the variables are typically chosen to be knowns. The command NCCollectOnVars itself has the option LeftsAndRights → True, which prints out a list containing two lists
{{l1,...,lt},{r1,...,rt}}
Here l1 is the left side of term 1 of ”collected polynomial”, and r1 is the right side of term 1 of ”collected polynomial”, etc. An example is
N CCollectOnV ars[X * *A * *B * *Z + Y * *A * *B * *Z + A * *X + A * *Y, {A, B}] = (X + Y ) * *A * *B * *Z + A * *(X + Y) .
with LeftsAndRights → False. When LeftsAndRights → True, the output is
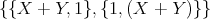
{{X + Y,1}, {1,(X + Y)}}
More detail is in 19.2.
Arguments: aListOfExpressions is a list of expressions. aListOfVariables is a list of variables.
Comments / Limitations: Not available before NCAlgebra1.2

In the example

N CCollectOnV ars[X * *A * *B * *Z + Y * *A * *B * *Z + A * *X + A * *Y,{A, B}] = (X + Y ) * *A * *B * *Z + A * *(X + Y ).
note that if we are in an environment where A and B have been set known and X,Y and Z are unknowns, then one may omit the list of variables {A,B} in the call above. In other words,
In[2]:= SetKnowns[A,B];  
In[3]:= SetUnknowns[X,Y,Z];  
In[4]:= NCCollectOnVars[X**A**B**Z + Y**A**B**Z + A**X+A**Y,{A,B}]  
 
Out[4] := (X+Y)**A**B**Z + A**(X+Y)

Another example is if A,Tp[A], B1, Tp[B1] B2, Tp[B2] C1, Tp[C1] C2 and Tp[C2] are knowns and all other variables are unknowns, then:

In[2] := long = E21 ** A ** iE21 ** E22 - E21 ** B1 ** Tp[B1] ** E12 +  
>    E21 ** B2 ** Tp[B2] ** E12 + E22 ** iE12 ** Tp[A] ** E12 -  
>    E21 ** B2 ** C1 ** iE21 ** E22 -  
>    E22 ** iE12 ** Tp[C1] ** Tp[B2] ** E12 +  
>    E21 ** B1 ** Tp[B1] ** E11 ** iE21 ** E22 -  
>    E21 ** B2 ** Tp[B2] ** E11 ** iE21 ** E22 -  
>    E22 ** iE12 ** E11 ** A ** iE21 ** E22 +  
>    E22 ** iE12 ** E11 ** B1 ** Tp[B1] ** E12 -  
>    E22 ** iE12 ** E11 ** B2 ** Tp[B2] ** E12 -  
>    E22 ** iE12 ** Tp[A] ** E11 ** iE21 ** E22 +  
>    E22 ** iE12 ** E11 ** B2 ** C1 ** iE21 ** E22 +  
>    E22 ** iE12 ** Tp[C1] ** Tp[B2] ** E11 ** iE21 ** E22 -  
>    E22 ** iE12 ** E11 ** B1 ** Tp[B1] ** E11 ** iE21 ** E22 +  
>    E22 ** iE12 ** E11 ** B2 ** Tp[B2] ** E11 ** iE21 ** E22  
 
In[3] := NCCollectOnVariables[long]  
 
Out[3]:= E22 ** iE12 ** Tp[A] ** (E12 - E11 ** iE21 ** E22) +  
>    (E21 - E22 ** iE12 ** E11) ** A ** iE21 ** E22 -  
>    (E21 - E22 ** iE12 ** E11) ** B1 ** Tp[B1] **  
>    (E12 - E11 ** iE21 ** E22) +  
>    (E21 - E22 ** iE12 ** E11) ** B2 ** Tp[B2] **  
>    (E12 - E11 ** iE21 ** E22) -  
>    E22 ** iE12 ** Tp[C1] ** Tp[B2] ** (E12 - E11 ** iE21 ** E22) -  
>    (E21 - E22 ** iE12 ** E11) ** B2 ** C1 ** iE21 ** E22

The NCCollectOnVars option LeftAndRight → True

This prints out a list containing two lists

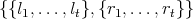
{{l1,...,lt},{r1,...,rt}}
Here l1 is the left side of term 1 of ”collected polynomial”, and r1 is the right side of term 1 of ”collected polynomial”, etc. In the example above the list of left sides is
 E22 ** iE12,  
>    (E21 - E22 ** iE12 ** E11),  
>    -(E21 - E22 ** iE12 ** E11),  
>    (E12 - E11 ** iE21 ** E22),  
>    (E21 - E22 ** iE12 ** E11),  
>    (E12 - E11 ** iE21 ** E22),  
>    -E22 ** iE12,  
>    -(E21 - E22 ** iE12 ** E11)

and the list of right sides is

{  
 (E12 - E11 ** iE21 ** E22), iE21 ** E22,  
-(E12 - E11 ** iE21 ** E22),  (E12 - E11 ** iE21 ** E22),  
 -  (E12 - E11 ** iE21 ** E22), - iE21 ** E22 }

The NCProcess option NCCV → True

If the NCProcess option NCCV → True is set NCProcess will perform the sort of collection described in Section 19.2. Specifically, NCCollectOnVars[ OutputofGroebnerBasisAlgorithms, KnownIndeterminates ] is called before the result is output to LATEX. This has been shown to be useful in the discovery of “motivated unknowns” as discussed in [HS].

19.3 Turning screen output off

In the notebook environment you will definitely want to turn a lot of NCProcess screen output off. Too much output drowns the notebook. In fact we are so sure of this that suppressing diagnostic output is the default. Turning it on or off or on is done with the Options

PrintScreenOutput → True
PrintScreenOutput → False

The default is   PrintScreenOutput → False

also see the command

NCGBMmaDiagnostics[ True]
NCGBMmaDiagnostics[ False]

which turns on (and off) more diagnostics.

19.4 Output Options

There are several options for NCProcess which determine the appearance of the output. These are actually options for the RegularOutput command which is called by NCProcess. Additional options for RegularOutput can be handed to RegularOutput with the NCProcess option AdditionalRegularOutputOptions → aList, where aList is a list of rules. The following options can be used directly as if they were NCProcess options. These three options are independent of one another. All three files can be created with one NCProcess call.

19.4.1 Turning screen output off: PrintScreenOutput→ False

In the notebook environment you will definitely want to turn a lot of NCProcess screen output off. Too much output drowns the notebook. Turning it off or on is done with the Option

PrintScreenOutput → False
PrintScreenOutput → True

The default is   PrintScreenOutput → False

19.4.2 TeX→ True

This option gives spreadsheets a LATEX appearance. The default is TeX → True.

There is a bug in the program to create spreadsheets. In the list of variables that have been solved for, the letter i is sometimes replaced by a number. The TEX file is absolutely correct. The bug only appears in a list of variables, never in an equation.

19.4.3 ASCII→ False

This option creates the spreadsheet in ascii text form. This is a lot more difficult to read, but it can be useful for copying and pasting relations from the spreadsheet into a Mathematica session. The default is ASCII → False.

19.4.4 NCGBFastRegularOutput→ False

If NCGBFastRegularOutput → True processing of equations done by NCProcess will be done by the C++ kernel rather than Mathematica. This is much faster, but not quite as pretty as with Mathematica. The default is NCGBFastRegularOutput → False. We hope this option is functional as of August 1999.

19.4.5 NCShortFormulas→-1

See Section 15.3.4.

19.5 NCProcess Summary Table

NCProcess[aListOfPolynomials, iter, “Filename”, Options]____________ UserSelect →{} Deselect →{}

MainUnknowns→{}

RR → True

RRByCat → False

SB → False

SBByCat → False

SBFlatOrder → False

DegreeCap →-1

DegreeSumCap →-1

NCCV→ True

This list of polynomials will appear in the UserSelects category in the file “Filename”. Polynomials in this list will not be used to do something or other. Indeterminates in this list will cause the output of NCProcess to only contain equations containing these indeterminates or functions of them. Setting RR → True will cause the algorithm to use RemoveRedundant to reduce partial Gröbner bases. RemoveRedundant is very fast. Specifies whether or not to use RemoveRedundantByCategory. This is slower than RemoveRedundant, but it is still fast. Specifies whether or not to use SmallBasis. This can be very slow. Specifies whether or not to use SmallBasisByCategory, which is a slower but more particular form of SmallBasis. This can be slow. Specifies whether or not to use NCFlatSmallBasis which takes the length lexicographic monomial order for the small basis algorithm. This might be faster than the above two options. Sets the DegreeCap for NCMakeGB within NCProcess. The DegreeCap for SmallBasis is set to one higher. -1 means there is no cap. Sets the DegreeSumCap for NCMakeGB within NCProcess. The DegreeSumCap for SmallBasis is set to one higher. Turns on NCCollectOnVariables, which collects on the knowns.
NCProcess options continued__________________________________

NCGBNag → True

NCShortFormulas→-1

TeX→ True

NCGBFastRegularOutput→ False

NCKnownIndeterminant→{}

DisplayOptions→{}

NCGBDebug→ False

PrintScreenOutput→ False

Setting NCGBNag → True will cause the current partial GB to be called into Mathematica, output to the screen and saved to a file after each iteration. Sets a maximum length for the expressions output by NCProcess. Longer relations will simply be eliminated. Eg. NCShortFormulas → 200. -1 means no expressions will be eliminated. Produces a TeX Spreadsheet, which pops up on the screen, if you are setup properly. Specifies whether or not to do processing of equations by the C++ kernel rather than Mathematica. This is much faster, but not quite as pretty as with Mathematica. An indeterminant in this list will only change the NCProcess display of knowns and unknowns. Indeterminants lower in the order than the ”group” containing the specified indeterminant will be regarded as known for purposes of sorting by categories in the NCProcess display. (Not implemented as of July 19, 1999) False turns off the beginning part of the spreadsheet which displays the input to NCProcess Creates lots of files that an NCProcess specialist can use to asses problems with the Mma paprts of NCProcess. Suppresses some NCProcess diagnostic output.

[next] [prev] [prev-tail] [front] [up]