[next] [prev] [prev-tail] [tail] [up]

Chapter 45
Sample Applications

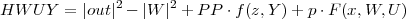
Each of the following examples uses one of the SYSDef files as input. That SYSDef file is reproduced here for your reference. Text between comment symbols (* and *) is non-executable. In this document we have modified the actual SYSDef files by a few deletions and by transcribing many of the comments to TeX. Everything else in the SYSDef file is loaded into your session when you type:

<<SYSDef####.m

where #### represents the particular SYSDef file chosen.

45.1 Bounded Real Lemma

This example derives the bounded real lemma for a linear system. You should see the notebook DemoBRL.ps and have the joy of executing DemoBRL.nb.

45.2 Measurement Feedback H∞ Control

We wish to analyse the dissipativity condition on 2 port systems with a one port system in feedback. The basic question is when does feedback exist which makes the full system dissipative and internally stable? This example is based on the paper [BHW]. Here is a listing of the definitions for a nonlinear system which is affine in the input. It is part of our SYS file named SYSDefIA.m - again here are TeX transcriptions:

INPUT AFFINE SYSTEM DEFINITIONS
(* file is SYSDefIA.m  
  This file loads in basic definitions of two systems and of  
the energy balance relations various connections of the  
systems satisfy.  
 
                     __________________  
                     |                |  
           W  ---->--|             G1 |---->--- out1  
                     |  F             |  
           U  ---->--|             G2 |---->--- Y  
                     |________________|  
                      ______________  
                      |            |  
            U  ----<--| g      f   |----<--- Y  
                      |____________|  
 
                         Figure 2.  
 
                 dx/dt  =  F[x,W,U]  
                  out1  =  G1[x,W,U]  
                    Y   =  G2[x,W,U]  
 
                 dz/dt  =  f[z,Y]  
                    U   =  g[z,Y]  
 
 An Input Affine (IA) one port system is  
---------------------------------------- *)  
                   SetNonCommutative[f,g,a,b,c,dd,z]  
 
                       f[z_,Y_]:=a[z]+b[z]**Y  
                       g[z_,Y_]:=c[z]+dd[z]**Y  
 
(* An Input Affine (IA) two port system is *)  
 
                   SetNonCommutative[W,U,Y,DW,DU,DY]  
                   SetNonCommutative[A,x,B1,B2,C1,C2,G1,G2]  
                   SetNonCommutative[D11,D22,D12,D21]  
                     D11[x_]:=0  
                     D22[x_]:=0  
 
                   F[x_,W_,U_]:=A[x]+B1[x]**W+B2[x]**U  
                   G1[x_,W_,U_]:=C1[x]+D11[x]**W+D12[x]**U;  
                            out1=G1[x,W,U];  
                   G2[x_,W_,U_]:=C2[x]+D21[x]**W+D22[x]**U;  
                            out2=G2[x,W,U];  
                            G2I[x_,Y_,U_]:=inv[D21[x]]**Y-inv[D21[x]]**C2[x];  

ENERGY BALANCE EQUATIONS

We begin with notation for analyzing the DISSIPATIVITY of the systems obtained by connecting f,g to F,G in several different ways. The energy function on the statespace is denoted by e. HWUY below is the Hamiltonian of the two decoupled systems where inputs are W,U, and Y.

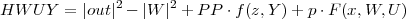
HW U Y = ∣out∣2 - ∣W ∣2 + PP ⋅f(z,Y) + p⋅F (x,W, U)
SetNonCommutative[F,G1,G2,f,g,p,PP];  
HWUY = tp[out1]**out1-tp[W]**W+  
                       (p**F[x,W,U]+tp[F[x,W,U]]**tp[p])/2+  
                                     (PP**f[z,Y]+tp[f[z,Y]]**tp[PP])/2;  

CONNECTING INPUT AND OUTPUT

If we connect the Y output of the 2 port to the f,g input then the resulting system has Hamiltonian function HWU.

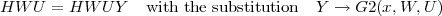
HW U = HW UY with the substitution Y → G2(x, W, U)
HWU=HWUY/.Y->G2[x,W,U];

If we connect the U input of the 2 port to the f,g output then the resulting system has Hamiltonian function HWY.

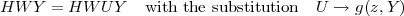
HW Y = HW U Y with the substitution U → g(z,Y )
HWY=HWUY/.U->g[z,Y];

If we connect the two systems in feedback, that is tie off U and Y, then the resulting Hamiltonian function is

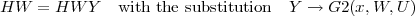
HW = HW Y with the substitution Y → G2(x,W, U )
HW=HWY/.Y->G2[x,W,U];

By definition (see Section I) the closed loop system being e-DISSIPATIVE corresponds to the energy balance function HW above being negative.

Note that the function HWUY contains both state and dual variables. Dual variables are defined by the gradient of the energy function, as follows:

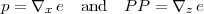
p = ∇x e and P P = ∇z e

In the following, when we impose the IA assumptions (see (1.5) and (1.6)), we will often specialize to a plant which satisfies

D11(x) = D22(x) = 0,
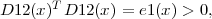
D12(x)T D12(x) = e1(x) > 0,
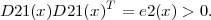
D21(x)D21(x)T = e2(x) > 0.
and a compensator with d(z)=0. We now write out energy balance formulas for the plant and compensator after Figure 2 (under these assumptions) purely in terms of state space variables x and z (designated by the prefix s for state space).
PURE STATESPACE VARIABLES

STATESPACE -x,z. While the HWUY formulas mix x’s and p ’s , the next ones are purely on statespace variables x and z. Executable formulas for

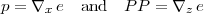
p = ∇x e and P P = ∇z e
are inserted by the rule
SNC[GEx,GEz];  
ruxz={p->tp[GEx[x,z]], PP->tp[GEz[x,z]]};

Here,

GEx[x,z], GEz[x,z]

stand for column vectors ∇xT e, ∇zT e, respectively. This unfortunate choice of notation is a holdover from earlier versions of the software.

The storage function e is homogeneous

          GEx[0,0]=0;  
          GEz[0,0]=0;  
 
sHWUY=HWUY/.ruxz;  
sHWU=HWU/.ruxz;  
sHWY=HWY/.ruxz;  
sHW=HW/.ruxz;

RESULTS STORED FOR FAST EXECUTION

The following are redundant in that they can be computed from the above expressions.

This is the W which maximizes Hamiltonian

ruCritW= {W -> tp[B1[x]] ** GEx[x, z]/2 +  
     tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/2}  
 
CritW[x_,z_,b_]:= tp[B1[x]] ** GEx[x, z]/2 +  
                tp[D21[x]] ** tp[b] ** GEz[x, z]/2;  
 
(*  and you get  *)  
 
sHWo = tp[A[x]] ** GEx[x, z]/2 + tp[C1[x]] ** C1[x] + tp[GEx[x, z]] ** A[x]/2 +  
  tp[GEz[x, z]] ** a[z]/2 + tp[a[z]] ** GEz[x, z]/2 +  
  tp[C1[x]] ** D12[x] ** c[z] + tp[C2[x]] ** tp[b[z]] ** GEz[x, z]/2 +  
  tp[GEx[x, z]] ** B2[x] ** c[z]/2 + tp[GEz[x, z]] ** b[z] ** C2[x]/2 +  
  tp[c[z]] ** e1[x] ** c[z] + tp[c[z]] ** tp[B2[x]] ** GEx[x, z]/2 +  
  tp[c[z]] ** tp[D12[x]] ** C1[x] +  
  tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
  tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4 +  
  tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
  tp[GEz[x, z]] ** b[z] ** e2[x] ** tp[b[z]] ** GEz[x, z]/4  
 
 
(* This is the U which minimizes Hamiltonian *)  
ruCritU = {U -> -inv[e1[x]] ** tp[B2[x]] ** GEx[x, z]/2 -  
     inv[e1[x]] ** tp[D12[x]] ** C1[x]};  
 
CritU[x_,z_]:=-inv[e1[x]] ** tp[B2[x]] ** GEx[x, z]/2 -  
     inv[e1[x]] ** tp[D12[x]] ** C1[x];  
 
 
END OF FILE  ############################################ END OF FILE

45.2.1 Derivation of CritW and sHWo

Now the demo starts by taking the Hamiltonian for the closed loop system sHW and optimizing it in W to get what we denote sHWo. Soon the demo requires serious knowledge of [BHW] so if the reader has problems he is urged to read SYSHinfTAC.m a file which gives a rather complete account of the terse and unmotivated calculations here.

In[4]:= <<SYStems.m  
 
NOTE: SYStems.m loads in the following files:  
      NCAlgbra.m, NCAliasFunctions.m, SYSDefIA.m,  
      SYSSpecialize.m, and SYSHinfFormulas.m  
 
In[5]:= Substitute[sHW,dd[z]->0]  
 
Out[5]= -tp[W] ** W + (tp[c[z]] ** tp[D12[x]] + tp[C1[x]]) **  
    (C1[x] + D12[x] ** c[z]) + ((tp[W] ** tp[B1[x]] + tp[c[z]] ** tp[B2[x]] +  
         tp[A[x]]) ** GEx[x, z] +  
      tp[GEx[x, z]] ** (A[x] + B1[x] ** W + B2[x] ** c[z]))/2 +  
   (tp[GEz[x, z]] ** (b[z] ** (C2[x] + D21[x] ** W) + a[z]) +  
      ((tp[W] ** tp[D21[x]] + tp[C2[x]]) ** tp[b[z]] + tp[a[z]]) ** GEz[x, z])  
     /2  
 
The critical W, found by taking the gradient of % and setting it to 0,  
is  
 
In[6]:= CriticalPoint[%,W]  
 
Out[6]= {W -> tp[B1[x]] ** GEx[x, z]/2 +  
     tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/2}  
 
In[7]:= Substitute[%%,%]  
 
Out[7]= -(tp[GEx[x, z]] ** B1[x]/2 + tp[GEz[x, z]] ** b[z] ** D21[x]/2) **  
     (tp[B1[x]] ** GEx[x, z]/2 + tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/2) +  
   (tp[c[z]] ** tp[D12[x]] + tp[C1[x]]) ** (C1[x] + D12[x] ** c[z]) +  
   (((tp[GEx[x, z]] ** B1[x]/2 + tp[GEz[x, z]] ** b[z] ** D21[x]/2) **  
          tp[B1[x]] + tp[c[z]] ** tp[B2[x]] + tp[A[x]]) ** GEx[x, z] +  
      tp[GEx[x, z]] ** (A[x] + B1[x] **  
          (tp[B1[x]] ** GEx[x, z]/2 + tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/2) \  
          + B2[x] ** c[z]))/2 +  
   (tp[GEz[x, z]] ** (b[z] ** (C2[x] +  
            D21[x] ** (tp[B1[x]] ** GEx[x, z]/2 +  
               tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/2)) + a[z]) +  
      (((tp[GEx[x, z]] ** B1[x]/2 + tp[GEz[x, z]] ** b[z] ** D21[x]/2) **  
             tp[D21[x]] + tp[C2[x]]) ** tp[b[z]] + tp[a[z]]) ** GEz[x, z])/2  
 
 
         ------Check this against the stored formula for sHWo  
In[8]:= NCExpand[%-sHWo]  
 
Out[8]= -tp[c[z]] ** e1[x] ** c[z] +  
   tp[c[z]] ** tp[D12[x]] ** D12[x] ** c[z] -  
   tp[GEz[x, z]] ** b[z] ** e2[x] ** tp[b[z]] ** GEz[x, z]/4 +  
   tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4  
 
In[9]:= Substitute[%%,rue]  
 
NOTE: rue = {tp[D12[x_]] ** D12[x_] :> e1[x], D21[x_] **  
             tp[D21[x_]] :> e2[x]}  
 
Out[9]= 0  

The output sHWo is also recorded in the file SYSDefIA.m above. Note that neither sHWo nor sHWoWIA depends on a or c.

45.2.2 The MIN/MAX in U

Also useful is the optimum CritU for

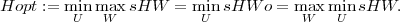
Hopt := miUnmaWx sHW = miUnsHW o = maWx minU sHW.

For WIA systems there is not an elegant formula for CritU and possibly is not unique. For IA systems, one gets the concrete formula:

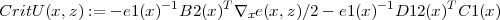
CritU (x,z) := - e1(x)- 1B2(x)T∇xe(x, z)∕2 - e1(x)- 1D12(x)T C1(x)

45.2.3 Derivations of IAX, Critc, and Hopt

Now we optimize sHWo in c[z] variable and restrict to x=z to get the Doyle Glover Kargonekar Francis condition for IA systems. Henceforth we abbreviate commands by their aliases.

In[4]:= <<SYStems.m  
In[5]:= Crit[sHWo,c[z]]  
 
Out[5]= {c[z] ->  
    -inv[e1[x]] ** tp[B2[x]] ** GEx[x, z]/2 -  
     inv[e1[x]] ** tp[D12[x]] ** C1[x]}      ----------- this is ruCritU  
In[6]:= Hopt = NCE[Sub[sHWo,%5]]  
 
Out[6]= tp[A[x]] ** GEx[x, z]/2 + tp[C1[x]] ** C1[x] +  
   tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** a[z]/2 +  
   tp[a[z]] ** GEz[x, z]/2 + tp[C2[x]] ** tp[b[z]] ** GEz[x, z]/2 +  
   tp[GEz[x, z]] ** b[z] ** C2[x]/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   tp[C1[x]] ** D12[x] ** inv[e1[x]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[C1[x]] ** D12[x] ** inv[e1[x]] ** tp[D12[x]] ** C1[x] +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[x]] ** tp[B2[x]] ** GEx[x, z]/4 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[x]] ** tp[D12[x]] ** C1[x]/2 +  
   tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEz[x, z]] ** b[z] ** e2[x] ** tp[b[z]] ** GEz[x, z]/4  
 
In[7]:= Sub[Hopt,x->z]  
 
Out[7]= tp[A[z]] ** GEx[z, z]/2 + tp[C1[z]] ** C1[z] +  
   tp[GEx[z, z]] ** A[z]/2 + tp[GEz[z, z]] ** a[z]/2 +  
   tp[a[z]] ** GEz[z, z]/2 + tp[C2[z]] ** tp[b[z]] ** GEz[z, z]/2 +  
   tp[GEz[z, z]] ** b[z] ** C2[z]/2 +  
   tp[GEx[z, z]] ** B1[z] ** tp[B1[z]] ** GEx[z, z]/4 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[z]] ** GEx[z, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] +  
   tp[GEx[z, z]] ** B1[z] ** tp[D21[z]] ** tp[b[z]] ** GEz[z, z]/4 -  
   tp[GEx[z, z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** GEx[z, z]/4 -  
   tp[GEx[z, z]] ** B2[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 +  
   tp[GEz[z, z]] ** b[z] ** D21[z] ** tp[B1[z]] ** GEx[z, z]/4 +  
   tp[GEz[z, z]] ** b[z] ** e2[z] ** tp[b[z]] ** GEz[z, z]/4  
 
In[8]:= ruXXYYI  
 
Out[8]= {GEz[x_, x_] :> 0, GEx[x_, x_] :> 2*XX[x], GEx[x_, 0] :> 2*YYI[x]}  
 
In[9]:= Sub[%7,%]  
 
Out[9]= tp[A[z]] ** XX[z] + tp[C1[z]] ** C1[z] + tp[XX[z]] ** A[z] +  
   tp[XX[z]] ** B1[z] ** tp[B1[z]] ** XX[z] -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[z]] ** XX[z] -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** XX[z] -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]  
 
In[10]:= NCE[%-IAX[z]]  
Out[10]= 0

45.2.4 Derivation of IAYI

This is an advanced exercise in the use of the glossary at the end of this document file. The glossary stores the basic formulas for solutions to the IA H∞ control problem. We use them here to familiarize the reader with the GLOSSARY.

In[4]:= <<SYStems.m  
 
In[5]:= Sub[sHWo,z->0]  
 
Out[5]= tp[A[x]] ** GEx[x, 0]/2 + tp[C1[x]] ** C1[x] +  
   tp[GEx[x, 0]] ** A[x]/2 + tp[GEz[x, 0]] ** a[0]/2 +  
   tp[a[0]] ** GEz[x, 0]/2 + tp[C1[x]] ** D12[x] ** c[0] +  
   tp[C2[x]] ** tp[b[0]] ** GEz[x, 0]/2 + tp[GEx[x, 0]] ** B2[x] ** c[0]/2 +  
   tp[GEz[x, 0]] ** b[0] ** C2[x]/2 + tp[c[0]] ** e1[x] ** c[0] +  
   tp[c[0]] ** tp[B2[x]] ** GEx[x, 0]/2 + tp[c[0]] ** tp[D12[x]] ** C1[x] +  
   tp[GEx[x, 0]] ** B1[x] ** tp[B1[x]] ** GEx[x, 0]/4 +  
   tp[GEx[x, 0]] ** B1[x] ** tp[D21[x]] ** tp[b[0]] ** GEz[x, 0]/4 +  
   tp[GEz[x, 0]] ** b[0] ** D21[x] ** tp[B1[x]] ** GEx[x, 0]/4 +  
   tp[GEz[x, 0]] ** b[0] ** e2[x] ** tp[b[0]] ** GEz[x, 0]/4  
 
In[6]:= ruhomog  
 
Out[6]= {A[0] -> 0, C1[0] -> 0, C2[0] -> 0, a[0] -> 0, c[0] -> 0}  
 
In[7]:= Sub[%%,ruhomog]  
 
Out[7]= tp[A[x]] ** GEx[x, 0]/2 + tp[C1[x]] ** C1[x] +  
   tp[GEx[x, 0]] ** A[x]/2 + tp[C2[x]] ** tp[b[0]] ** GEz[x, 0]/2 +  
   tp[GEz[x, 0]] ** b[0] ** C2[x]/2 +  
   tp[GEx[x, 0]] ** B1[x] ** tp[B1[x]] ** GEx[x, 0]/4 +  
   tp[GEx[x, 0]] ** B1[x] ** tp[D21[x]] ** tp[b[0]] ** GEz[x, 0]/4 +  
   tp[GEz[x, 0]] ** b[0] ** D21[x] ** tp[B1[x]] ** GEx[x, 0]/4 +  
   tp[GEz[x, 0]] ** b[0] ** e2[x] ** tp[b[0]] ** GEz[x, 0]/4  
 
In[8]:= Sub[%,ruXXYYI]  
 
NOTE: ruXXYYI = {GEz[x_, x_] :> 0, GEx[x_, x_] :> 2 XX[x],  
                 GEx[x_, 0] :> 2 YYI[x]}  
 
Out[8]= tp[A[x]] ** YYI[x] + tp[C1[x]] ** C1[x] + tp[YYI[x]] ** A[x] +  
   tp[C2[x]] ** tp[b[0]] ** GEz[x, 0]/2 + tp[GEz[x, 0]] ** b[0] ** C2[x]/2 +  
   tp[YYI[x]] ** B1[x] ** tp[B1[x]] ** YYI[x] +  
   tp[GEz[x, 0]] ** b[0] ** D21[x] ** tp[B1[x]] ** YYI[x]/2 +  
   tp[GEz[x, 0]] ** b[0] ** e2[x] ** tp[b[0]] ** GEz[x, 0]/4 +  
   tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** tp[b[0]] ** GEz[x, 0]/2  
 
In[9]:= SubSym[%,ruqb]  
 
NOTE: ruqb = tp[b[z_]] ** GEz[x_, z_] :> q[x, z]  
 
Out[9]= tp[A[x]] ** YYI[x] + tp[C1[x]] ** C1[x] + tp[C2[x]] ** q[x, 0]/2 +  
   tp[YYI[x]] ** A[x] + tp[q[x, 0]] ** C2[x]/2 +  
   tp[q[x, 0]] ** e2[x] ** q[x, 0]/4 +  
   tp[YYI[x]] ** B1[x] ** tp[B1[x]] ** YYI[x] +  
   tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** q[x, 0]/2 +  
   tp[q[x, 0]] ** D21[x] ** tp[B1[x]] ** YYI[x]/2  
 
In[10]:= Crit[%,q[x,0]]  
 
Out[10]= {q[x, 0] ->  
    -2*inv[e2[x]] ** C2[x] - 2*inv[e2[x]] ** D21[x] ** tp[B1[x]] ** YYI[x]}  
 
In[11]:= Sub[%%,%]  
 
Out[11]= (-2*tp[C2[x]] ** inv[e2[x]] -  
       2*tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]]) ** C2[x]/2 +  
   tp[A[x]] ** YYI[x] + tp[C1[x]] ** C1[x] +  
   tp[C2[x]] ** (-2*inv[e2[x]] ** C2[x] -  
       2*inv[e2[x]] ** D21[x] ** tp[B1[x]] ** YYI[x])/2 +  
   tp[YYI[x]] ** A[x] + (-2*tp[C2[x]] ** inv[e2[x]] -  
       2*tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]]) ** e2[x] **  
     (-2*inv[e2[x]] ** C2[x] - 2*inv[e2[x]] ** D21[x] ** tp[B1[x]] ** YYI[x])/  
    4 + (-2*tp[C2[x]] ** inv[e2[x]] -  
       2*tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]]) ** D21[x] **  
     tp[B1[x]] ** YYI[x]/2 + tp[YYI[x]] ** B1[x] ** tp[B1[x]] ** YYI[x] +  
   tp[YYI[x]] ** B1[x] ** tp[D21[x]] **  
     (-2*inv[e2[x]] ** C2[x] - 2*inv[e2[x]] ** D21[x] ** tp[B1[x]] ** YYI[x])/  
    2  
 
In[12]:= NCE[%]  
 
Out[12]= tp[A[x]] ** YYI[x] + tp[C1[x]] ** C1[x] + tp[YYI[x]] ** A[x] -  
   tp[C2[x]] ** inv[e2[x]] ** C2[x] +  
   tp[YYI[x]] ** B1[x] ** tp[B1[x]] ** YYI[x] -  
   tp[C2[x]] ** inv[e2[x]] ** D21[x] ** tp[B1[x]] ** YYI[x] -  
   tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]] ** C2[x] -  
   tp[YYI[x]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]] ** D21[x] ** tp[B1[x]] **  
    YYI[x]  
 
In[13]:= NCE[%-IAYI[x]]  
 
Out[13]= 0

45.2.5 Derivation of critical q, k, and bterm

In[2]:= <<SYStems.m  
 
In[3]:= SubSym[sHWo,ruc]  
 
NOTE: ruc = c[z_] :> -inv[e1[z]] ** (tp[B2[z]] ** XX[z] +  
            tp[D12[z]] ** C1[z])  
 
Out[3]= tp[A[x]] ** GEx[x, z]/2 + tp[C1[x]] ** C1[x] +  
   tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** a[z]/2 +  
   tp[a[z]] ** GEz[x, z]/2 + tp[C2[x]] ** tp[b[z]] ** GEz[x, z]/2 +  
   tp[GEz[x, z]] ** b[z] ** C2[x]/2 -  
   (tp[C1[z]] ** D12[z] + tp[XX[z]] ** B2[z]) ** inv[e1[z]] ** tp[B2[x]] **  
     GEx[x, z]/2 - (tp[C1[z]] ** D12[z] + tp[XX[z]] ** B2[z]) **  
    inv[e1[z]] ** tp[D12[x]] ** C1[x] -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] **  
    (tp[B2[z]] ** XX[z] + tp[D12[z]] ** C1[z]) +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] **  
     (tp[B2[z]] ** XX[z] + tp[D12[z]] ** C1[z])/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4 +  
   tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   (tp[C1[z]] ** D12[z] + tp[XX[z]] ** B2[z]) ** inv[e1[z]] ** tp[D12[x]] **  
    D12[x] ** inv[e1[z]] ** (tp[B2[z]] ** XX[z] + tp[D12[z]] ** C1[z]) +  
   tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4  
 
In[4]:= NCE[SubSym[%,rua]]  
 
NOTE: rua = a[z_] :> A[z] + B2[z] ** (-inv[e1[z]] **  
            (tp[B2[z]] ** XX[z] + tp[D12[z]] ** C1[z]))  
            - b[z] ** C2[z] + ((B1[z] - b[z] ** D21[z]) **  
            tp[B1[z]]) ** XX[z]  
 
Out[4]= tp[A[x]] ** GEx[x, z]/2 + tp[A[z]] ** GEz[x, z]/2 +  
   tp[C1[x]] ** C1[x] + tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** A[z]/2 +  
   tp[C2[x]] ** tp[b[z]] ** GEz[x, z]/2 -  
   tp[C2[z]] ** tp[b[z]] ** GEz[x, z]/2 + tp[GEz[x, z]] ** b[z] ** C2[x]/2 -  
   tp[GEz[x, z]] ** b[z] ** C2[z]/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEz[x, z]] ** B1[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[XX[z]] ** B1[z] ** tp[B1[z]] ** GEz[x, z]/2 -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z] -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 +  
   tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   tp[GEz[x, z]] ** b[z] ** D21[z] ** tp[B1[z]] ** XX[z]/2 -  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** tp[b[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] +  
   tp[GEz[x, z]] ** b[z] ** D21[x] ** tp[D21[x]] ** tp[b[z]] ** GEz[x, z]/4 +  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] ** D12[x] ** inv[e1[z]] **  
    tp[B2[z]] ** XX[z] + tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] **  
    D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] +  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] ** D12[x] ** inv[e1[z]] **  
    tp[B2[z]] ** XX[z] + tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] **  
    D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]  
 
In[5]:= SubSym[%,tp[GEz[x,z]]**b[z]->q[x,z]]  
 
Out[5]= q[x, z] ** C2[x]/2 - q[x, z] ** C2[z]/2 + tp[A[x]] ** GEx[x, z]/2 +  
   tp[A[z]] ** GEz[x, z]/2 + tp[C1[x]] ** C1[x] +  
   tp[C2[x]] ** tp[q[x, z]]/2 - tp[C2[z]] ** tp[q[x, z]]/2 +  
   tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** A[z]/2 +  
   q[x, z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   q[x, z] ** D21[x] ** tp[D21[x]] ** tp[q[x, z]]/4 -  
   q[x, z] ** D21[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[q[x, z]]/4 +  
   tp[GEz[x, z]] ** B1[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[XX[z]] ** B1[z] ** tp[B1[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** tp[q[x, z]]/2 -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z] -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] +  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] ** D12[x] ** inv[e1[z]] **  
    tp[B2[z]] ** XX[z] + tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] **  
    D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] +  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] ** D12[x] ** inv[e1[z]] **  
    tp[B2[z]] ** XX[z] + tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] **  
    D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]  
 
In[6]:= SubSym[%,rue]  
 
NOTE: rue = {tp[D12[x_]] ** D12[x_] :> e1[x], D21[x_] **  
             tp[D21[x_]] :> e2[x]}  
 
Out[6]= q[x, z] ** C2[x]/2 - q[x, z] ** C2[z]/2 + tp[A[x]] ** GEx[x, z]/2 +  
   tp[A[z]] ** GEz[x, z]/2 + tp[C1[x]] ** C1[x] +  
   tp[C2[x]] ** tp[q[x, z]]/2 - tp[C2[z]] ** tp[q[x, z]]/2 +  
   tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** A[z]/2 +  
   q[x, z] ** e2[x] ** tp[q[x, z]]/4 +  
   q[x, z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   q[x, z] ** D21[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[q[x, z]]/4 +  
   tp[GEz[x, z]] ** B1[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[XX[z]] ** B1[z] ** tp[B1[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** tp[q[x, z]]/2 -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z] -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] +  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** e1[x] ** inv[e1[z]] ** tp[B2[z]] **  
    XX[z] + tp[C1[z]] ** D12[z] ** inv[e1[z]] ** e1[x] ** inv[e1[z]] **  
    tp[D12[z]] ** C1[z] + tp[XX[z]] ** B2[z] ** inv[e1[z]] ** e1[x] **  
    inv[e1[z]] ** tp[B2[z]] ** XX[z] +  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** e1[x] ** inv[e1[z]] ** tp[D12[z]] **  
    C1[z]  
 
In[7]:= Crit[%,tp[q[x,z]]]  
 
Out[7]= {tp[q[x, z]] ->  
    -2*inv[e2[x]] ** C2[x] + 2*inv[e2[x]] ** C2[z] -  
     inv[e2[x]] ** D21[x] ** tp[B1[x]] ** GEx[x, z] +  
     2*inv[e2[x]] ** D21[z] ** tp[B1[z]] ** XX[z]}  
 
In[8]:= K=NCE[SubSym[%19,%20]]  
 
 
Out[8]= tp[A[x]] ** GEx[x, z]/2 + tp[A[z]] ** GEz[x, z]/2 +  
   tp[C1[x]] ** C1[x] + tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** A[z]/2 -  
   tp[C2[x]] ** inv[e2[x]] ** C2[x] + tp[C2[x]] ** inv[e2[x]] ** C2[z] +  
   tp[C2[z]] ** inv[e2[x]] ** C2[x] - tp[C2[z]] ** inv[e2[x]] ** C2[z] +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEz[x, z]] ** B1[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[XX[z]] ** B1[z] ** tp[B1[z]] ** GEz[x, z]/2 -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z] -  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z] -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] -  
   tp[C2[x]] ** inv[e2[x]] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/2 +  
   tp[C2[x]] ** inv[e2[x]] ** D21[z] ** tp[B1[z]] ** XX[z] +  
   tp[C2[z]] ** inv[e2[x]] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/2 -  
   tp[C2[z]] ** inv[e2[x]] ** D21[z] ** tp[B1[z]] ** XX[z] -  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]] ** C2[x]/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]] ** C2[z]/2 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEx[x, z]] ** B2[x] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** XX[z]/2 -  
   tp[GEz[x, z]] ** B2[z] ** inv[e1[z]] ** tp[D12[z]] ** C1[z]/2 +  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** inv[e2[x]] ** C2[x] -  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** inv[e2[x]] ** C2[z] -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[x]] ** GEx[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[B2[z]] ** GEz[x, z]/2 -  
   tp[XX[z]] ** B2[z] ** inv[e1[z]] ** tp[D12[x]] ** C1[x] +  
   tp[C1[z]] ** D12[z] ** inv[e1[z]] ** e1[x] ** inv[e1[z]] ** tp[B2[z]] **  
    XX[z] + tp[C1[z]] ** D12[z] ** inv[e1[z]] ** e1[x] ** inv[e1[z]] **  
    tp[D12[z]] ** C1[z] - tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] **  
     inv[e2[x]] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]] ** D21[z] **  
     tp[B1[z]] ** XX[z]/2 + tp[XX[z]] ** B1[z] ** tp[D21[z]] ** inv[e2[x]] **  
     D21[x] ** tp[B1[x]] ** GEx[x, z]/2 -  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** inv[e2[x]] ** D21[z] ** tp[B1[z]] **  
    XX[z] + tp[XX[z]] ** B2[z] ** inv[e1[z]] ** e1[x] ** inv[e1[z]] **  
    tp[B2[z]] ** XX[z] + tp[XX[z]] ** B2[z] ** inv[e1[z]] ** e1[x] **  
    inv[e1[z]] ** tp[D12[z]] ** C1[z]  
 
In[9]:= K = NCC[NCC[K,inv[e2[x]]],inv[e1[z]]]  
 
Out[9]= tp[A[x]] ** GEx[x, z]/2 + tp[A[z]] ** GEz[x, z]/2 +  
   tp[C1[x]] ** C1[x] + tp[GEx[x, z]] ** A[x]/2 + tp[GEz[x, z]] ** A[z]/2 +  
   (tp[GEx[x, z]] ** B2[x] + tp[GEz[x, z]] ** B2[z]) ** inv[e1[z]] **  
    (-tp[B2[z]] ** XX[z]/2 - tp[D12[z]] ** C1[z]/2) +  
   (tp[C1[z]] ** D12[z] + tp[XX[z]] ** B2[z]) ** inv[e1[z]] **  
    (-tp[B2[x]] ** GEx[x, z]/2 - tp[B2[z]] ** GEz[x, z]/2 -  
      tp[D12[x]] ** C1[x]) + tp[C2[x]] ** inv[e2[x]] **  
    (-C2[x] + C2[z] - D21[x] ** tp[B1[x]] ** GEx[x, z]/2 +  
      D21[z] ** tp[B1[z]] ** XX[z]) +  
   (tp[XX[z]] ** B1[z] ** tp[D21[z]] + tp[C2[z]]) ** inv[e2[x]] **  
    (C2[x] - C2[z] + D21[x] ** tp[B1[x]] ** GEx[x, z]/2 -  
      D21[z] ** tp[B1[z]] ** XX[z]) +  
   tp[C1[x]] ** D12[x] ** inv[e1[z]] **  
    (-tp[B2[z]] ** XX[z] - tp[D12[z]] ** C1[z]) +  
   tp[GEx[x, z]] ** B1[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
   tp[GEz[x, z]] ** B1[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[XX[z]] ** B1[z] ** tp[B1[z]] ** GEz[x, z]/2 +  
   (tp[C1[z]] ** D12[z] + tp[XX[z]] ** B2[z]) ** inv[e1[z]] ** e1[x] **  
    inv[e1[z]] ** (tp[B2[z]] ** XX[z] + tp[D12[z]] ** C1[z]) +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** inv[e2[x]] **  
    (-C2[x]/2 + C2[z]/2 - D21[x] ** tp[B1[x]] ** GEx[x, z]/4 +  
      D21[z] ** tp[B1[z]] ** XX[z]/2)  
 
In[10]:= qpart = NCE[%19-(%19//.q[x,z]->0)]  
 
Out[10]= q[x, z] ** C2[x]/2 - q[x, z] ** C2[z]/2 +  
   tp[C2[x]] ** tp[q[x, z]]/2 - tp[C2[z]] ** tp[q[x, z]]/2 +  
   q[x, z] ** e2[x] ** tp[q[x, z]]/4 +  
   q[x, z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   q[x, z] ** D21[z] ** tp[B1[z]] ** XX[z]/2 +  
   tp[GEx[x, z]] ** B1[x] ** tp[D21[x]] ** tp[q[x, z]]/4 -  
   tp[XX[z]] ** B1[z] ** tp[D21[z]] ** tp[q[x, z]]/2  
 
In[11]:= %//.tp[q[x,z]]->0  
 
Out[11]= q[x, z] ** C2[x]/2 - q[x, z] ** C2[z]/2 +  
   q[x, z] ** D21[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   q[x, z] ** D21[z] ** tp[B1[z]] ** XX[z]/2  
 
In[12]:= L = %//.q[x,z]->1  
 
Out[12]= C2[x]/2 - C2[z]/2 + D21[x] ** tp[B1[x]] ** GEx[x, z]/4 -  
   D21[z] ** tp[B1[z]] ** XX[z]/2  
 
In[13]:= Q = e2[x]/4  
 
Out[13]= e2[x]/4  
 
In[14]:= bterm = q[x,z]+tp[L]**inv[Q]  
 
Out[14]= 4*(tp[GEx[x, z]] ** B1[x] ** tp[D21[x]]/4 -  
       tp[XX[z]] ** B1[z] ** tp[D21[z]]/2 + tp[C2[x]]/2 - tp[C2[z]]/2) **  
     inv[e2[x]] + q[x, z]  
 
In[15]:= Sub[NCE[%19-bterm**Q**tp[bterm]-K],rue]  
 
Out[15]= 0  
 
In[16]:= Quit

45.3 Specializing to less general systems

45.3.1 Specializing to linear systems

To specialize to the linear case, just apply

∙   rulinearsys to make the systems linear

∙   rulinearEB to make the energy function quadratic

∙   ruGE1 then ruGEXY to make the energy function solve the Hinf problem (max entropy soln.)

∙   rulinearall contains all of the rules above and is what we usually use.

(See Glossary)

45.3.2 Specializing Using The Doyle Glover Khargonekar Francis Simplifying Assumptions

A special class of IA systems are those satisfying

D12(x)TC1(x) = 0 and B1(x)D21(x)T = 0
denoted in this paper as the Doyle-Glover-Kargonekar-Francis (DGKF) simplifying assumptions (see [DGKF]). These simplify algebra substantially so are good for tutorial purposes even though they are not satisfied in actual control problems. Look for rules ruDGKF*.

(See Glossary)

45.3.3 Demo: Linear Doyle Glover Kargonekar Francis Equations

The following demo verifies IAX and IAYI are same as DGX DGYI the Doyle Glover X and inv[Y] Riccati equations in the special case of a linear system.

In[24]:= <<SYStems.m  
 
In[25]:= NCE[IAX[x]//.rulinearall]  
 
Out[25]= tp[x] ** XX ** A ** x + tp[x] ** tp[A] ** tp[x] ** XX +  
   tp[x] ** tp[C1] ** C1 ** x + tp[x] ** XX ** B1 ** tp[B1] ** tp[x] ** XX -  
   tp[x] ** XX ** B2 ** inv[e1] ** tp[B2] ** tp[x] ** XX -  
   tp[x] ** XX ** B2 ** inv[e1] ** tp[D12] ** C1 ** x -  
   tp[x] ** tp[C1] ** D12 ** inv[e1] ** tp[B2] ** tp[x] ** XX -  
   tp[x] ** tp[C1] ** D12 ** inv[e1] ** tp[D12] ** C1 ** x  
 
In[26]:= Sub[%,x->1]  
 
Out[26]= XX ** A + tp[A] ** XX + tp[C1] ** C1 + XX ** B1 ** tp[B1] ** XX -  
   XX ** B2 ** inv[e1] ** tp[B2] ** XX -  
   XX ** B2 ** inv[e1] ** tp[D12] ** C1 -  
   tp[C1] ** D12 ** inv[e1] ** tp[B2] ** XX -  
   tp[C1] ** D12 ** inv[e1] ** tp[D12] ** C1  
 
In[27]:= NCE[%-DGX]  
 
Out[27]= 0  
 
In[28]:= NCE[IAYI[x]//.rulinearall]  
 
Out[28]= tp[x] ** inv[YY] ** A ** x + tp[x] ** tp[A] ** tp[x] ** inv[YY] +  
   tp[x] ** tp[C1] ** C1 ** x - tp[x] ** tp[C2] ** inv[e2] ** C2 ** x +  
   tp[x] ** inv[YY] ** B1 ** tp[B1] ** tp[x] ** inv[YY] -  
   tp[x] ** inv[YY] ** B1 ** tp[D21] ** inv[e2] ** C2 ** x -  
   tp[x] ** tp[C2] ** inv[e2] ** D21 ** tp[B1] ** tp[x] ** inv[YY] -  
    tp[x] ** inv[YY] ** B1 ** tp[D21] ** inv[e2] ** D21 ** tp[B1] ** tp[x] **  
    inv[YY]  
 
In[29]:= Sub[%,x->1]  
 
Out[29]= inv[YY] ** A + tp[A] ** inv[YY] + tp[C1] ** C1 -  
   tp[C2] ** inv[e2] ** C2 + inv[YY] ** B1 ** tp[B1] ** inv[YY] -  
   inv[YY] ** B1 ** tp[D21] ** inv[e2] ** C2 -  
   tp[C2] ** inv[e2] ** D21 ** tp[B1] ** inv[YY] -  
   inv[YY] ** B1 ** tp[D21] ** inv[e2] ** D21 ** tp[B1] ** inv[YY]  
 
In[30]:= NCE[YY**%**YY-DGY]  
 
Out[32]= 0  
 
In[34]:= Quit

[next] [prev] [prev-tail] [front] [up]