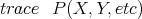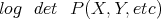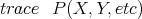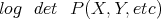Part I
NCAlgebra

If you would like to try the NCAlgebra package or want updates go to the NCAlgebra web site

or contact   ncalg@ucsd.edu or MathSource@wri.com.

The basic NCAlgebra program was written by the authors and David Hurst, Daniel Lamm, Orlando Merino, Robert Obarr, Henry Pfister, Stan Yoshinobu, Phillipe Bergman, Dell Kronewitter, and Eric Rowell. Various additions include contributions by Dave Glickstein, Juan Camino, Jeff Ovall, Tony Mendes, and Tony Shaheen. The Mathematica C++ hybrid was developed with Kurt Schneider, Victor Shih and Mike Moore. Control demos are coauthored with Mike Walker. Simplification commands are based on theory developed by Bill Helton, John Wavrik and Mark Stankus. The beginnings of the program come from eran@slac. This program was written with support from the AFOSR, the NSF, the Lab for Mathematics and Statistics at UCSD, the UCSD Faculty Mentor Program and the US Department of Education.

0.1 ReleaseNotes NCAlgebra

ReleaseNotes NCAlgebra 4.0 January 2010

Code has been cleaned up and improved. Basic functionality is supported without changes.

ReleaseNotes NCAlgebra 3.7 Sept. 2002

Convexity We changed some defaults and fixed some bugs in NCConvexityRegion and NCMatrixOfQuadratic. Now it runs quickly on fairly big problems.

Path Setting Paths were set to make NCAlgebra more path independent.

CSP Our support for Control System Professional was updated to accomodate the second (2002) version of CSP.

ReleaseNotes NCAlgebra 3.5 Sept. 2001

Basic Changes You no longer have to set every variable to be noncommutative. We have a command NCGuts which has an option called NCSetNC. When set to True, all letters are automatically noncommutative unless SetCommutative makes them commutative.

A further option of NCGuts allows one to use “**” to multiply matrices with noncommutative entries – the more cumbersome MatMult command is no longer needed. While this option seems dangerous to Bill, it makes many computations prettier and easier to type. If you don’t trust the answer, then don’t use the option.

Commands For Matricies With Noncommuting Entries We now have an LDU decomposition for matricies with noncommuting entries. Also, there is a command for computing the inverse of such matrices (however this only works under strong assumptions).

NCMatrixOfQuadratic gives a vector matrix factorization of a symmetric quadratic noncommutative function.

A Second Derivative Command NCHessian computes the Hessian of a function with noncommuting variables and coefficents.

Computing The Region Where A Noncommutative Function is Convex NCConvexityRegion is a command used to determine the region of formal noncommutative inequalities where a given noncommutative function is convex.

NCGuts: NCGuts holds set of options geared for simplifying transposing, finding the inverse, and multiplying matrices conaining noncommuting variables.

NCStrongProduct1 - > False is the first option of NCGuts. When True, ** serves to multiply matrices with noncommutative entries as well as maintaining its original function. In addition, tp[ ] and tpMat are the same. The default setting is True.

NCStrongProduct2 - > False is the second option of NCGuts. When set to True, if M is a matrix with noncommutative entries, inv[M] returns a formula expression for the inverse of M. NCStrongProduct2 forces NCStrongProduct1.

NCSetNC - > False is the last option of NCGuts. When set to True, all letters are automatically noncommutative unless SetCommutative makes them commutative. This replaces the need for repeated calls to SetNonCommutative.

NCLDUDecomposition: Given a square matrix M with noncommutative entries, this command finds the LDU decomposition of M. It returns a list of four elements, namely L,D,U, and P such that PXP^T = LDU. The first element is the lower triangular matrix L, the second element is the diagonal matrix D, the third element is the upper triangular matrix U, and the fourth is the permutation matrix P (the identity is returned if no permutation is needed). As an option, it may also return a list of the permutations used at each step of the LDU factorization as a fifth element.

NCAllPermutationLDU: NCAllPermutationLDU returns the LDU decomposition of a matrix after all possible column permutations are applied. The code cycles through all possible permutations and calls NCLDUDecomposition for each one. As an option, the permutations used for each LDU decomposition can also be returned.

NCMatrixOfQuadratic: NCMatrixOfQuadratic gives a vector matrix factorization of a symmetric quadratic noncommutative function. A three element list is the output. The first element is the left border vector, the second element is a symmetric coefficent matrix, and the third is the right border vector. The border vectors contain the variables in the given quadratic function and their transposes.

NCIndependenceCheck: NCIndependenceCheck verifies whether or not a given set of polynomials are independent or not. It analyzes each list of polynomials separately. There are three possible types of outputs for each list. Two of them correspond to NCIndependenceCheck successfully determining whether or not the list of polynomials is independent. The third type of output corresponds to an unsuccessful attempt at determining dependence or independence.

NCBorderVectorGather: NCBorderVectorGather can be used to gather the polynomial coefficents preceeding the elements given in a list of variables whenever they occur.

NCPermutationMatrix: NCPermutationMatrix returns the permutation matrix associated with the list of the first n integers. It gives the identity matrix with its columns re-ordered.

NCMatrixToPermutation: NCMatrixToPermutation returns the permutation associated with the permutation matrix, aMatrix. It is the inverse of NCPermutationMatrix.

NCInverse: NCInverse gives a symbolic inverse of a matrix with noncommutative entries.

NCHessian: NCHessian computes the Hessian of a function with noncommuting variables and coefficents. This is a second directional derivative which can be thought of as the second order term in the noncommutative Taylor expansion. Output will be a symmetric quadratic function with respect to the directions of differentiation.

NCConvexityRegion: This command is used to determine the region of formal noncommutative inequalities where a given noncommutative function is convex. NCConvexityRegion preforms three main operations. Given a noncommutative function F, the Hessian of F is computed with NCHessian. Then, using NCMatrixOfQuadratic, the Hessian is factored into vector matrix vector form. Finally, NCAllPermutationLDU finds the LDU decomposition of the symmetric coefficent matrix. The diagonal elements in the diagonal matrix in the LDU decomposition is returned.

ReleaseNotes NCAlgebra 3.0

NCAlgebra 3.0 has several added functions.

1. LDU decomposition for block matices, to include a block Cholesky decompsition.
2. Formulas for inverses of block matrices.
3. A command which differentiates functions of the form
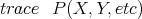
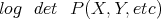
4. Support for the Mathematica toolbox Control System Professional. It gives CSP the ability to handle non-commuting objects.
5. A function which represents elements of an algebra as n×n matrices with commuting symbolic entries, or with inegers.
6. Online Help - While we have not set up help browsers at this time in the Mma style, one can get searchable online help by viewing NCBIGDOCUMENT.html with Netscape, etc. When you are in an NCAlgebra session just keep a web browser open with NCBIGDOCUMENT.html loaded in. The powerfulsearch features of these browsers allow you to look up things in the document.

An X in commands, e.g. NCXetc., always means that this command is experimental and we reserve the right to change it.