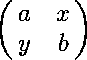
| 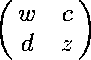
|
|---|
last modified Jul 2, 1996
Given matrices a, b, c and d, we wish to determine under what conditions there exists matrices x, y, z and w such that the block two by two matrices
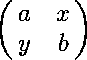
| 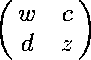
|
|---|
This problem was solved in a paper by W.W. Barrett, C.R. Johnson, M. E. Lundquist and H. Woerderman [BJLW] where they showed it splits into several cases depending upon which of a, b, c and d are invertible. In our next example, we assume that a, b, c and d are invertible and derive the result which they obtain. In the Mathematica input file MatrixInverseInput.m we run NCProcess1 on the polynomial equations which state that a, b, c and d are invertible together with the eight polynomial equations which come from the two matrices above being inverses of each other. What we get is the following spreadsheet:
THE ORDER IS NOW THE FOLLOWING:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| YOUR SESSION HAS DIGESTED | ||
|---|---|---|
| THE FOLLOWING RELATIONS | ||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
| USER CREATIONS APPEAR BELOW | ||
|---|---|---|
| SOME RELATIONS WHICH APPEAR BELOW | ||||
|---|---|---|---|---|
| MAY BE UNDIGESTED | ||||
This spreadsheet shows that, if a, b, c and d are invertible, then one can find x, y, z and w such that the matrices above are inverses of each other if and only if z b z = z + d a c. The spreadsheet also gives formulas for x, y and w in terms of z. In [BJLW] they also solve the problem in the case that a is not invertible --- the answer is more complicated and involves conditions on ranks of certain matrices. It is not clear whether or not these can be derived in a purely algebraic fashion.