last modified Jul 3, 1996
Unitary case of Parrot's Lemma
We begin by stating Parrot's Lemma.
Lemma [Y]
Let a be an m x m matrix,
c an n x m matrix and d an
n x n matrix. There exists an m x n matrix
z such that
is a contraction if and only if
Since we can not handle inequalities,
we analyze the case where
the unknown matrix z must be chosen to make
the matrix above unitary.
Per our usual advice, when just starting a problem, we take
most matrices to be invertible. Since only a and
d are square, we assume that a and d are invertible.
If a and d are invertible, then
the matrix above is unitary if
and only if the following polynomials are zero.
Notice that all of these equations do not need to be typed in. The
input for this run can be seen in
ParrotStep1.m.
When we run NCProcess1 on these equations, we obtain
this spreadsheet.
Since the spreadsheet
contains the equations
the equation
follows from
the above spreadsheet.
The above spreadsheet and the observation just made
shows that, if a, c
and d are invertible, then
there exists a matrix z such that
the matrix
above is unitary if and only if
Moreover, if z exists, then
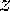


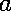
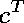
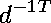
To show that
under the above invertibility assumptions,
there exists an m x n matrix z such that
the matrix
above
is unitary if and only if
it is necessary
to show that the equation
follows
from the equations in the spreadsheet which do
not involve either
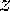 or
or
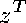 .
.
One can either
show this by hand or run NCProcess1 on the equations
in the above spreadsheet which do not involve
either
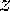 or
or
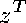 together with
the equation
together with
the equation
and see that this equation is redundant.
which reduces to
In summary,
if a, c and d are invertible,
there exists a matrix z such that
the matrix
above is unitary if and only if
Since we assumed that a and d were invertible, the above
calculation has a ``back of the envelope'' flavor.
Now that our ``back of the envelope'' calculation assuming
invertibility
was successful, it is easy to remove the invertibility assumptions.
If we do not assume that a and d are invertible,
NCProcess1
produces this
spreadsheet.
One could use these equations to push through
to the unitary case of Parrot's Lemma.
However, since the theorem is well known, there is not much point
in publishing this derivation.
Notice from the
spreadsheet
above that if d is invertible,
then one can solve for z. So far, we only have a result
for the case that both a and d are invertible. Let
us consider the case when only d is invertible and
see what happens.
If we do not assume that
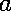 or
or
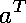 is invertible, but do
assume that
is invertible, but do
assume that
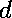 is invertible (and so, of course, assume that
is invertible (and so, of course, assume that
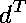 is invertible), then we obtain the this
spreadsheet.
is invertible), then we obtain the this
spreadsheet.
Notice the last expression in the spreadsheet.
This equation can be factored to
Therefore, the matrix a is onto. Since a is a square matrix,
a is invertible.
Thus, by using the spreadsheet and
the special properties of matrices (rather than elements
of an arbitrary abstract algebra) we have discovered that
if d is invertible, then a is invertible.
At this point in the session we would add the fact
that
a is invertible, run NCProcess1 and one would obtain the
first
spreadsheet.
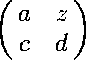
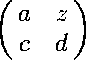
![]() or
or
![]() together with
the equation
together with
the equation