NCProcess commands

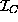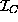The idealized operations Categorize and Decompose cannot be implemented on a computer. There are two difficulties with implementing an approximation to the the Categorize operation. The first difficulty is that a computer cannot generate the ideal . The second difficulty is that if a human is presented with a large subset of the ideal , then looking for ``interesting'' polynomials to place in 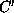can be overwhelming.

The NCProcess commands approximate the Categorize and Decompose operations and address the two difficulties mentioned above. This paper studies two such commands, NCProcess1 and NCProcess2. NCProcess1 functions as follows:

(1) NCProcess1 takes as input a set C of polynomial equations. Some of these equations may be marked ``important''. These important equations are in the set 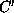mentioned in §.

(2) NCProcess1 takes the set C and computes a different set of polynomial equations by running the noncommuting Gröbner Basis algorithm. The Gröbner Basis Algorithm hopefully eliminates unknowns.

(3) NCProcess1 then attempts to find smaller subsets of the set created in item 2 which generate the same ideal. The way in which NCProcess1 find smaller subsets is described in § and in [NCGBDoc].

(4) NCProcess1 then takes the small generating set from item 3 and ``factors'' each polynomial in a way which suggests possible decompositions to the users.

The NCProcess command is described further in §.

Item 4 above is the best approximation which we know to the Decompose operation. The notion of factoring mentioned in item 4 is different from the standard one and is explained in §.

As a final step we run NCProcess2 which aggressively eliminates redundant equations and partitions the output equations in a way which facilitates proving that the necessary conditions are also sufficient. In terms of the list above, NCProcess2 carries out items 3 and 4, but not item 2. NCProcess2 uses a more aggressive algorithm for item 3 than NCProcess1 uses.

The output from the NCProcess commands is displayed along the lines of the Categorize operation: NCProcess displays all of the output equations in one unknown together, two unknowns together, etc. For a more detailed description of the output, see §.