Noncommutative elimination theory

Those already knowledgeable about computer algebra know that an important classical property of commutative Gröbner Basis concerns elimination ideals. If G is a Gröbner Basis with respect to an elimination order (see Definition 11.2) and I is the ideal generated by G, then there exist a nested sequence of ideals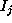

such that 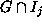is a Gröbner Basis for 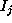. In §, we generalize this to the noncommutative case. This result is crucial to assuring that the Gröbner Basis algorithm puts the collection of polynomial equations into a triangular form. Pure lex and, more generally, multigraded lex are examples of such elimination orders.