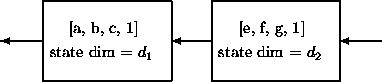
Definition A factorization
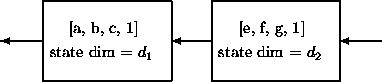
of a system [A,B,C,1] is minimal if the statespace
dimension of [A,B,C,1] is 
.
Theorem([BGKvD])
Minimal factorizations
of a system [A,B,C,1]
correspond to
projections 
and 
satisfying 
,
We begin by giving the algebraic statement of the problem. Suppose that these factors exist. By the Youla-Tissi statespace isomorphism theorem, there is map
which intertwines the
original and the product system.
Also minimality of the factoring is equivalent to
the existence of a two-sided inverse 
to 
.
These requirements combine to imply that
each of the expressions of (FAC) below is zero.
