


Next: Example: Solving the Control
Up: Computing decompositions
Previous: NCCollectOnVariables
As in the introduction
(§),
suppose we are in a context where there are knowns
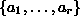 and unknowns
and unknowns
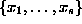 .
We now describe how we shall
be using the NCCV command to help discover
decompositions. (In the forthcoming example
(see
§),
Step 3 below is easy
enough that it is done by inspection.
No run of the GBA is required.)
NCCV can be used as follows:
.
We now describe how we shall
be using the NCCV command to help discover
decompositions. (In the forthcoming example
(see
§),
Step 3 below is easy
enough that it is done by inspection.
No run of the GBA is required.)
NCCV can be used as follows:
- (1) Apply NCCV to a polynomial p
and pay
particular attention to
the terms containing the most knowns. That is,
for each term, compute the degree of that term with
respect to the set of knowns and use the ones
with the highest degree in this sense.
- (2)
The collected form of p may suggest a decomposition
of p or suggest that there is another polynomial in the ideal
which has a decomposition. Let us suppose that one of the
the parenthesized summands of the collected form of
p has a decomposition as
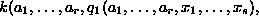
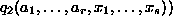 .
Therefore, we obtain
.
Therefore, we obtain
(5.7)
p =
k(a , ...,
a
, ...,
a ,
q
,
q (a
(a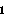 , ...,
a
, ...,
a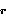 ,
x
,
x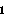 , ...,
x
, ...,
x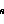 ),
q
),
q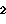 (a
(a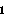 , ...,
a
, ...,
a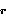 ,
x
,
x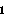 , ...,
x
, ...,
x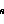 )) +
s
)) +
s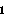
from this operation where k is a polynomial
and
s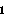 is a
polynomial.
is a
polynomial.
- (3) Declare both of the new variables
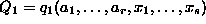 and
and
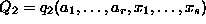 ,
set
,
set 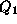 and
and 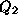 lower in the ordering
than all other unknowns and run the GBA.
This
will convert (5.7) to
lower in the ordering
than all other unknowns and run the GBA.
This
will convert (5.7) to
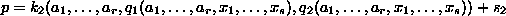
If 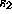 contains no unknowns, then we have found the desired decomposition.
contains no unknowns, then we have found the desired decomposition.
For example, if, in a computer session, A, B,
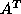 and
and 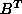 are set to be knowns and
b, d,
are set to be knowns and
b, d, 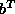 and
and 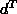 are set to be unknowns, then
are set to be unknowns, then
(5.8)
1 - d
d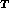 +
B
+
B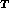 (b
d
(b
d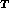 - (1 + b
b
- (1 + b
b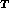 )
B) + d
b
)
B) + d
b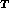 B - (d -
B
B - (d -
B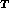 b)
A
b)
A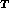 A
(b
A
(b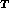 B -
d
B -
d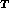 )
)
is the output of NCCollectOnVariables when applied to
(5.5).
This suggests we set 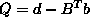 and
and 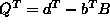 .
Step 3 above
converts (5.8) to
.
Step 3 above
converts (5.8) to
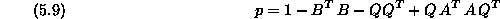
which gives the decomposition 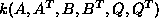 for p as described in
Example
5.4.
for p as described in
Example
5.4.
Helton
Wed Jul 3 10:27:42 PDT 1996
![]() , ...,
a
, ...,
a![]() ,
q
,
q![]() (a
(a![]() , ...,
a
, ...,
a![]() ,
x
,
x![]() , ...,
x
, ...,
x![]() ),
q
),
q![]() (a
(a![]() , ...,
a
, ...,
a![]() ,
x
,
x![]() , ...,
x
, ...,
x![]() )) +
s
)) +
s![]()
![]() is a
polynomial.
is a
polynomial.
![]()
![]() contains no unknowns, then we have found the desired decomposition.
contains no unknowns, then we have found the desired decomposition.