End game

Now let us compare what we have found to the well known solution of (HGRAIL). In that theory there are two Ricatti equations due to Doyle, Glover, Khargonekar and Francis. These are the DGKF X and Y equations. One can read off that the equation which we found is the DGKF equation for , while the Ricatti equation which we just analyzed is the DGKF X equation.

Indeed what we have proved is that if (HGRAIL) has a solution with invertible and if b and c are given by formulas (6.11) and (6.13), then

(1) the DGKF X and 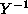equations must have a solution

(2) X and Y are self-adjoint

(3) 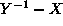is invertible

Now we turn to the converse. The straightforward converse of the above italicized statement would be: If items (1), (2) and (3) above hold, then (HGRAIL) has a solution with invertible and b and c are given by formulas (6.11) and (6.13). There is no reason to believe (and it is not the case) that b and c must be given by the formulas (6.11) and (6.13). These two formulas came about in § and were motivated by ``excess freedom'' in the problem. The converse which we will attempt to prove is:

Proposed Converse 6.14 If items (1), (2) and (3) above hold, then (HGRAIL) has a solution with invertible.

To obtain this proposed converse, we need a complete spreadsheet corresponding to the last stages of our analysis. The complete spreadsheet is:

THE ORDER IS NOW THE FOLLOWING:
A < A < B < B < B < B < C < C < C < C < X < X < Y < Y « E « E « E « E « E « E « E « E « E « E « E « E « E « E « E « E « b « b « c « c « a « a

	YOUR SESSION HAS DIGESTED
	THE FOLLOWING RELATIONS

THE FOLLOWIN VARIABLES HAVE NOT BEEN SOLVED FOR:
{a, b, c, E, E, a, b, c, E, E, E, E, E, E, E, E}
The corresponding rules are the following:

a -E A E + E C B E + E C B E + E E B B E - E C C E E - E E B C E E - E C B E E E - E E B B E E E

b -E C - E E B

c -B E + C E E + B E E E

E Y

E Y

a -E A E + E B C E + E B C E + E B B E E - E E C C E - E E E B C E - E E C B E E - E E E B B E E

b -C E - B E E

c -E B + E E C + E E E B

E E

E E

E E

E E

E E

E E

E E

E E

The expressions with unknown variables {}
and knowns {A, B, B, C, C, X, Y, X, Y, A, B, B, C, C}

X X 1

Y Y 1

X X 1

Y Y 1

Y B C Y A + A Y + C C - C C - C B Y

X B B X X A + A X - X B C - C B X + X B B X

	USER CREATIONS APPEAR BELOW

E Y

E E E E - X

	SOME RELATIONS WHICH APPEAR BELOW
		MAY BE UNDIGESTED

THE FOLLOWING VARIABLES HAVE NOT BEEN SOLVED FOR:
{E, E, E, E, E, E}
The expressions with unknown variables {E, E}
and knowns {}

E E 1

E E 1

The expressions with unknown variables {E, E}
and knowns {}

E E 1

E E 1

The expressions with unknown variables {E, E}
and knowns {}

E E 1

E E 1

The expressions with unknown variables {E, E, E, E}
and knowns {X} E E E E - X

In the spreadsheet, we use conventional X, notation rather than ``discovered'' notation so that our arguments will be familiar to experts in the field of control theory.

Now we use the above spreadsheet to verify the proposed converse. To do this, we assume that matrices A, , , , , X and Y exist, that X and Y is invertible, that X and Y are self-adjoint, that is invertible and that the DGKF X and equations hold. That is, the two following polynomial equations hold.

We wish to assign values for the matrices , , , , a, b and c such that each of the equations on the above spreadsheet hold. If we can do this, then each of the equations from the starting polynomial equations from § will hold and the proposed converse will follow.

(1) Note that all of the equations in the -Category of the above spreadsheet hold since X and Y solve the DGKF equations and are both invertible.

(2) Set equal to the inverse of Y. This assignment is dictated by the user selects. Note that follows since Y is self-adjoint.

(3) Let and be any invertible matrices such that . For example, one could choose and to both be the identity matrix.

(4) Note that there is there is a user select and that , are invertible. Since is invertible and , are invertible. Therefore, we set . Since , and , it follows that is invertible and self-adjoint.

(5) Since has been set for i,j=1,2, we can set a, b and c according to their formulas at the top of the spreadsheet .

With the assignments of , , , , a, b and c as above, it is easy to verify by inspection that every polynomial equation on the spreadsheet above holds.

We have proven the proposed converse and, therefore, have proven the following approximation to the classical [DGKF] theorem.

Theorem 6.15 If (HGRAIL) has a solution with invertible and b and c are given by the formulas (6.11) and (6.13), then the DGKF X and Y equations have solutions X and Y which are symmetric matrices with X, Y and Y - X invertible. The DGKF X and Y equations have solutions X and Y which are symmetric matrices with X, Y and Y - X invertible, then (HGRAIL) has a solution with invertible .

Note that we obtained this result with an equation in the one unknown X and an equation with the one unknown . From the strategy point of view, the first spreadsheet featured an equation in the single unknown b (and its transpose) and an equation in the single unknown c (and its transpose) and so is the most complicated. For example, the (6.10) decomposes as

where and is a symmetric polynomial which does not involve b. This forces us to say that the proof of the necessary side of theorem 6.15 was done with a 2-strategy.

A more aggressive way of selecting knowns and unknowns allows us to obtain this same result with a symmetrized 1-strategy. In particular, one would set a, b and c to be the only unknowns to obtain a first spreadsheet. The first spreadsheet contains key equations like (6.16) which is a symmetric 1-decomposition because does not contain a, b or c. Once we have solved for a, b and c, we turn to the next spreadsheet by declaring the variables involving (e.g., , , ...) to be unknown. At this point, the computer run is the same as Steps 2, 3 and 4 above.