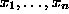over a field K as in
§.
Once a term order is defined, one can define the notion
of a leading term, leading monomial and leading coefficient
of a nonzero polynomial p. If p is a polynomial,
and 
is a monic monomial,
then 
is the leading term of p
if appears as a term of p and for every
term c M of p (with 
and M a monic monomial), is greater than
or equal to M in the term order. In this case,
is called the leading coefficient of p and
is called the leading monomial of p.
For a nonzero polynomial f, let lt(f)
denote the leading term of f (with
respect
to the given ordering),
lc(f) denote the leading
coefficient of f and
lm(f) denote the leading monomial of f.
Note that lt(f)=lc(f) lm(f).