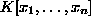denote the set of
(noncommutative) polynomials in
the indeterminates 
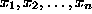over a field K.
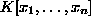is a noncommutative algebra.
Let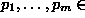 
,
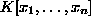C be a set of polynomials
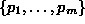and
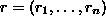with each
.
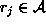If r is a common zero of
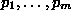, then r is a
zero of every polynomial p which lies in the smallest
ideal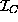 
generated by C.
Furthermore,
if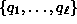 
is a generating set for
the ideal ,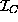
then r is a common zero of the p's if
and only if it is a common zero of the q's.
These ideas are learned by most mathematics undergraduates
in the case that the indeterminates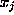 
lie in a commutative algebra
and they also hold when the 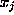lie in a noncommutative algebra.
The practical value of doing this algebraic manipulation is
that
instead of trying to solve for the common zeros
of 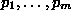directly, it could be advantageous
to find a different set
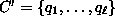of polynomials
which generates the same ideal
as 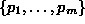and then solve for
the common zeros on the q's.
For example, 
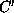might consist of
decoupled polynomial equations
which could be solved numerically (say using Matlab)
while the original set C produces numerically intractable problems.
The reader who is interested in seeing examples at this point might decide to skip directly to §.