


Next: The SmallBasis Operation
Up: Finding a small generating
Previous: The need to consider
Example
12.1
shows that, in some cases, we seek a minimal generating set
for an ideal;
Example
12.3
shows that in some cases we prefer certain minimal
generating sets for an ideal to other minimal generating sets;
Example
12.4
shows that in some cases we prefer finding
small generating sets.
The choice of how to shrink a generating set is further complicated
by the desire to have shrinking occur quickly on the computer.
The remainder of this section describes six different operations
to convert from
a particular basis for an ideal to a smaller one.
They differ in approach, speed and functionality.
We now give a brief description of each of these
six operations.
- (1)
SmallBasis can be used
to find smaller generating sets and is
relatively fast. SmallBasis is described in
§.
SmallBasis uses the GBA heavily.
- (2)
ShrinkBasis is used to find all
minimal generating sets and can be very slow.
ShrinkBasis is often too slow to use in practice.
ShrinkBasis is described in
§.
ShrinkBasis uses the GBA heavily.
- (3)
RemoveRedundant is used to find smaller
generating sets and is very fast.
The RemoveRedundant
operation is described in
§.
The Remove Redundant operation requires the recording
of information during the previous
run of the GBA and uses that
information once the run is completed. For this reason,
the explanation of Remove Redundant requires some
initial theoretical discussions which are in
§.
The run time of Remove Redundant is very fast since it implements
a graph search and does not invoke a GBA.
- (4,5)
The fourth and fifth operations are
SmallBasis By Category and Remove Redundant By Category.
These two operations find smaller subsets while
respecting the fact that retaining polynomials
which do not involve unknowns is desirable and
they act on each category
individually.
These last two operations
are described in
§.
These two operations use SmallBasis and
RemoveRedundant, respectively, heavily.
- (6) The sixth operation is RemoveRedundantProtect.
This command combines the results
of three Remove Redundant runs and is very fast.
This command
is used to prevent equations not involving unknowns
from being removed by polynomials which involve unknowns.
Also, the command prevents
digested polynomials from being removed by
polynomials which are undigested.
This command is described in
§.
Recall, for the remainder of the section, that the ideal in 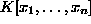 generated by
generated by
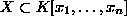 is denoted
is denoted 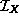 .
.



Next: The SmallBasis Operation
Up: Finding a small generating
Previous: The need to consider
Helton
Wed Jul 3 10:27:42 PDT 1996
![]() generated by
generated by
![]() is denoted
is denoted ![]() .
.