Definition 12.6
Let G = (V,E) be a graph such that
.
We say that G is a Gröbner graph if G is a directed acyclic
graph and for every v
V, either T(v,G) is the empty set or v lies in the ideal generated
by T(v,G).
Definition 12.7 Let G = (V,E) be a graph and v be a vertex of G. We will say that v is a starting vertex if T(v,G) is the empty set.
The following proposition follows easily from the previous two definitions and mathematical induction. We omit the proof.
Proposition 12.8
Let G = (V,E) be a Gröbner graph, V be a finite set and v be
a vertex of G. Let
be the set of starting vertices of G. Every element of V lies in the
ideal generated by
.
Remark 12.9 The hypothesis of Proposition 12.8 can be strengthened. One can replace the hypothesis that V be a finite set with the hypothesis that every element of V has only finitely many ancestors.
If one takes a subgraph 
of a Gröbner graph G = (V,E) such that
if v is a vertex of the graphthenand v is not a starting vertex of
is a Gröbner graph. Other subgraphs
of a Gröbner graph may
be Gröbner, but the above mentioned subgraphs can
be seen to be Gröbner from purely graph-theoretic
arguments.
We call these subgraphs subGröbner and
formalize this with the following definition.
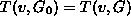
Definition 12.10
A graph G = (V,E) will be called a subGröbner graph
with respect to a Gröbner graph
if G is a subgraph a
and for every v
V, either v is a starting vertex of G or T(v,G) = T(v,
).
Note that if one is given a Gröbner graph
and a set of vertices
, then there is a smallest graph
G=(V,E) such that 
and G
is subGröbner with respect to .
If
and
are graphs, then we let
denote the graph
and let 
denote the graph 
.
Lemma 12.11
Let
be a Gröbner graph. If
and
are subGröbner with respect to
, then
is subGröbner with respect to
and
where
denotes the set of starting vertices of
for any Gröbner graph
.
Proof. \
For ease of reference, let 
,
and
. We wish to show that
. Since 
,
and 
, it suffices
to show that 
if and only if 
under the
conditions that 
,
or 
.
If , then
if and only if
,
if and only if
and
. Therefore,
if and only if
which occurs if and only if .
If , then
if and only if ,
and
.
Therefore,
if and only if
which occurs if and only if .
If , then
, if and only
if and
.
Therefore,
if and only if
which occurs if and only if .
In summary,
.
Let v be a vertex of 
which is not a starting vertex.
Therefore, 
.
Without loss of generality, assume that
. But then
and
. Therefore,
and so
Therefore, 
.
This completes the proof of Lemma
12.11.
The following lemma follows trivially from the definition of immediate ancestor, the definition of a starting vertex (Definition 12.7) and the definition of subGröbner graph (Definition 12.10).
Lemma 12.12
Let
be a Gröbner graph. If
=
and
=
are subGröbner with respect to
,
then
is subGröbner with respcet to
.
The following technical lemma will be used in the proof of Proposition prop:generating:RR
Lemma 12.13
Let
= (V,E) be a Gröbner graph,
be a finite set,
and for each
,
let
if
is and element of
such that
card(
)
card(
)
for each
,
then
is empty for every starting vertex w of
.
Proof. \
Suppose, for the purpose of proof by contradiction, that there
exists a starting vertex of w of such
that
is not empty.
Since is not empty, there exists
which is subGröbner with
respect to
such that
v is a vertex of 
and every starting vertex
of is a member of 
.
By Lemma
12.11,
is subGröbner with respect to and
.
By the choice of , the
fact that is a subgraph of
and the
fact that ,
the graph
equals the graph and so
must be a subgraph of . But
then, since 
,
w is a starting vertex of and w is a
vertex of , w is a member of 
which is a contradiction. Thus
is empty
for every
starting vertex of w of .
This completes the proof of Lemma 12.13.