Idealized shrinking by category

A protection against removing valuable polynomial equations is to not use the fact that the polynomial equations from a few categories may imply equations from a different category. This includes the case when two equations involving unknowns yield an equation involving only knowns. Certainly, if NCProcess finds an equation involving knowns, then this equation should be retained.

Recall that a spreadsheet consists of

(1) Polynomial equations which solve for a variable.

(2) Polynomial equations which do not involve any unknowns.

(3) User selected and user created polynomial equations.

(4) Undigested polynomials.

The equations in (1), (2) and (3) above were referred to as digested equations. These items were displayed in terms of a list of smaller sets of equations called categories. This division of a set of polynomial equations into categories suggests the following possible ways to shrink a set of polynomial equations while preserving important equations.

I. Let 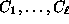be the categories. The simplest way is to replace 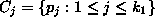with a minimal set 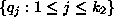such that the 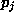's and the 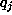's generate the same ideal.

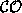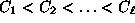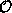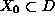II. The most drastic way to shrink is to pick an ordering on categories of undigested polynomial equations (for example, the one induced by the ordering underlying the run) and output the subset and 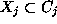defined to satisfy

(1) A minimal generating set for the digested polynomials D. Call it .

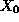(2) A minimal set of the form 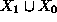which is a generating set for the ideal generated by the union of the digested polynomials D and the category .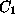

(3) A minimal set of the form 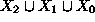which is a generating set for the ideal generated by the union of the digested polynomial D and the categories 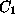and .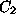

(4) etc.

Here D is the set of digested polynomials.

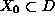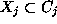III. An intermediate course which is less sensitive to ordering is to output the subset and defined to satisfy

(1) A minimal generating set for the digested polynomials D. Call it .

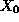(2) A minimal set of the form 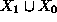which is a generating set for the ideal generated by the union of the digested polynomials D and the category .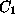

(3) A minimal set of the form 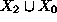which is a generating set for the ideal generated by the union of the digested polynomials D and the category .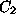

(4) etc.

Here D is the set of digested polynomials.