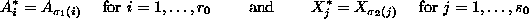in conjunction with problems involving an algebra which
possessed an involution, 
. We now make
this notion precise.
We start by assuming that there is an involution
on the
coefficients, say
.
By relabelling the knowns and unknowns if necessary, let us suppose that
and upon the
unknowns 
where 
and 
.
and does not depend on the unknowns 
.
Let us also suppose that there is
an injective map 
from
to 
and
an injective map 
from
to 
where and .
We now make the assumption which corresponds to the problem involving the algebra with involution:
If the mathematical problem we are trying to investigate involves elements of an algebraThere is a unique operationwith involution, say
for
and
for
for
and for
, then
from
to
such that the following four conditions hold:
is additive (i.e., if 
, then
).
, then
.
for 
.
for 
.