Formal description of multigraded lex

To specify a multigraded lex order on monic monomials in the variables x, ..., x such that 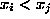if 1 i j n, then one needs to specify a subset of 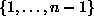. If M and N are monic monomials in the variables 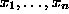, then M is less than N with respect to the multigraded lex order if one of the following two conditions hold:

(1)

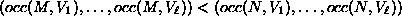
(2) 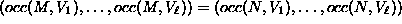and M is less than N with respect to the graded lex order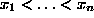

where

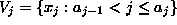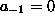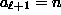(a) (we set and ) for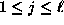

(b) occ(M,V) is the sum of occ(M,v) for all .

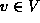To denote the above order, we write down the sequence of characters

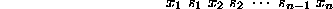
where 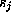is ``«'' if j is one of the 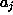's and 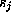is ``<'' otherwise.

Note that if the collection of subsets is the empty set, then the multigraded lex order is graded lex and if the collection of subsets is {1, 2, ..., n - 1}, then the multigraded lex order is a pure lex order.

As another example, a multigraded lex order for monic monomials in a, b, c, d and e such that a<b<c<d<e can be specified by specifying the set {2, 4}. This multigraded lex order would be denoted a < b « c < d « e

[BGK] H. Bart, I. Gohberg and M. A. Kaashoek, Minimal factorization of matrix and operator functions, Birkhäuser, 1979.

[BJLW] W. W. Barrett, C. R. Johnson, and M. E. Lundquist, H. Woerderman, ``Completing a Block Diagonal Matrix with a Partially Prescribed Inverse'', Linear Algebra Appl. 223/224 (1995), 73-87

[CLS] D. Cox, J. Little, D. O'Shea, Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, Springer-Verlag, Undergraduate Texts in Mathematics, 1992.

[DGKF] J. C. Doyle, K. Glover, P. P. Khargonekar and B. A. Francis, ``State-space solutions to standar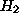d and 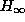control problems'', IEEE Trans. Auto. Control 34 (1989), 831-847.

[HW] J. W. Helton and J. J. Wavrik ``Rules for Computer Simplification of the formulas in operator model theory and linear systems'', Operator Theory: Advances and Applications 73 (1994), pp. 325--354.

[FMora] F. Mora, ``Groebner Bases for Non-commutative Polynomial Rings'' Lecture Notes in Computer Science, number 229 (1986) pp 353-362.

[FaFeGr] D. R. Farkas, C. D. Feustel and E. L. Green, ``Synergy in the theories of Gröbner Bases and Path Algebras'', Can. J. Math. 45(4), 1993 pp. 727-739.

[HSW] J. W. Helton, M. Stankus and J. J. Wavrik, ``Computer Simplification of Engineering Formulas''. , submitted to IEEE Trans. Auto. Control.

[NCA] J.W. Helton, R.L. Miller and M. Stankus, ``NCAlgebra: A Mathematica Package for Doing Non Commuting Algebra'' available from ncalg@ucsd.edu.

[NCGBDoc] J.W. Helton and M. Stankus, `NonCommutative Gröbner Basis Package'' available from ncalg@ucsd.edu

[TMora] T. Mora, ``An introduction to commutative and noncommutative Gröbner Bases'', Theoretical Computer Science, Nov 7,1994, vol. 134 N1:131-173.

[Y] N. Young,An introduction to Hilbert space., Cambridge Mathematical Textbooks. Cambridge University Press, 1988.