Solving the HGRAIL using NCProcess: Step 3
The starting polynomial equations for this step will be the
output from the first call to
NCProcess1
as well as the
four new equations
that we have just derived.
We ran NCProcess1 for two iterations.
Once again we go directly to the
spreadsheet which
NCProcess1 created.
There is no need to record all of it here, since at this
stage we shall
be concerned only with the undigested polynomial equations.
There are only
two undigested polynomial equations which are not banal.
The expressions with unknown variables
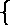

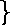
and knowns
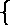
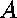

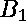

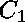

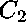

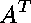

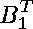

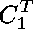

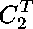

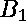
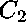


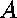

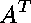


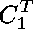
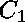

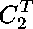
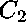

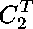
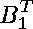

The expressions with unknown variables
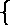








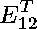

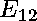
and knowns
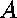

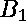

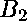

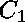

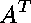

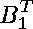

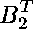

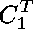


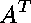
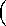
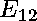




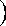

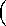




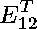
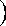
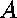



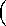




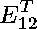
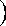
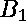
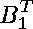
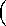
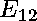




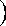

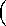




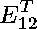
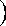
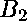
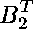
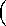
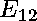




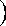



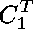
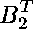
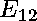









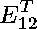
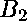
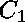



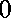
Step 4
Now we analyze these two polynomial equations.
The first polynomial equation is a
(Ricatti-Lyapunov) equation in
 .
Numerical methods for solving Ricatti equations
are common.
For this reason assuming that a Ricatti equation has a solution is a
socially acceptable
necessary condition throughout control
engineering.
Thus we can consider
.
Numerical methods for solving Ricatti equations
are common.
For this reason assuming that a Ricatti equation has a solution is a
socially acceptable
necessary condition throughout control
engineering.
Thus we can consider
 .
to be known.
.
to be known.
A first glance at the second equation reveals
that the same products of unknowns appear over and over.
Also we can see that this equation is symmetric. It would not take an
experienced person long to realize that by multiplying this
equation on the left by
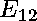
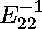 and on the right by
and on the right by
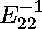
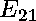 ,
we will have an equation in one unknown.
Now we can replace
,
we will have an equation in one unknown.
Now we can replace
with a new
variable X. This yields
Observe that this is an equation in the one unknown X.
End game
Now let us compare what we have found to the well known
solution of (HGRAIL).
In that theory there are two Ricatti equations due to Doyle,
Glover, Khargonekar and Francis.
These are the DGKF X and Y equations.
One can read off that the
 equation which we found is the DGKF
equation for
equation which we found is the DGKF
equation for
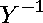 ,
while the Ricatti equation which we just analyzed
is the DGKF
,
while the Ricatti equation which we just analyzed
is the DGKF
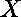 equation.
equation.
Indeed what we have proved is that if (HGRAIL) has a solution
with
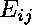 invertible and if b and c
are given by formulas
derived in
Step 2,
then
invertible and if b and c
are given by formulas
derived in
Step 2,
then
- the DGKF
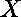 and
and
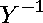 ,
equations must have a solution
,
equations must have a solution
-
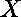 and
and
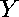 are self-adjoint
are self-adjoint
-
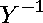

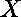 is invertible
is invertible
All that remains is to prove the converse



![]() .
Numerical methods for solving Ricatti equations
are common.
For this reason assuming that a Ricatti equation has a solution is a
socially acceptable
necessary condition throughout control
engineering.
Thus we can consider
.
Numerical methods for solving Ricatti equations
are common.
For this reason assuming that a Ricatti equation has a solution is a
socially acceptable
necessary condition throughout control
engineering.
Thus we can consider
![]() .
to be known.
.
to be known.
![]()
![]() and on the right by
and on the right by
![]()
![]() ,
we will have an equation in one unknown.
Now we can replace
,
we will have an equation in one unknown.
Now we can replace
![]() invertible and if b and c
are given by formulas
derived in
Step 2,
then
invertible and if b and c
are given by formulas
derived in
Step 2,
then
![]() and
and
![]() ,
equations must have a solution
,
equations must have a solution
![]() and
and
![]() are self-adjoint
are self-adjoint
![]()
![]()
![]() is invertible
is invertible