Orbits of U(n,n) acting on Mn: Step 2

The spreadsheet from Step 1 motivated us to introduce two new variables.

We will also defined the transposes of these two variables.

These new variables are declared as unknown, and place in the order directly above the knowns. This means that the algorithm will try to solve for the other unknowns in terms of f and F as well as the knowns x and y. The ordering for the second step looks like this.

For the second step we will use the actual Mathematica result of the first NCProcess run. This result was called ans1. We will take the union of our new definitions and ans1 to be the starting relations for the second NCProcess run. This is all done in the file OrbitStep2.m.

The entire spreadsheet is available, but here are a few things to notice.

First of all, two of our original unkowns have been solved for.

Evidently, F is invertible.

Two other interesting equations appear in the undigested section. The first one involves f and Tp[f].

The expressions with unknown variables

and knowns

There is a similar equation involving F and Tp[F].

The expressions with unknown variables

and knowns

As it turns out, this is the ``answer''. We can factor these two equations and we can see that f and F correspond to w and w which we described in equations (1) and (2). Thus we have obtained the following theorem.

Theorem: Suppose y and x are invertible and y is in the orbit of x under a linear fractional transformation

which satisfies the following conditions.

		.
Let m and m be defined as
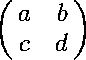
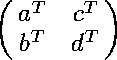m and m satisfy

where
.

then there exist w and w

as in (1) and (2).

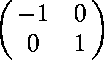The converse of this theorem remains to be settled. This question is related to the equations which we obtained as output of NCProcess but we did not look at. The next step is to figure out which of these equations we can eliminate.