last modified Jul 26, 1996
Sum of Three Idempotents Equals A Constant
The problem is to classify k idempotents
in an algebra
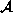 whose sum is equal to a
constant
whose sum is equal to a
constant
 I, where I is the identity.
As we shall see, the case of
three idempotents can be completely resolved using algebra, indeed
using NCAlgebra. It is known in various cases that if k is equal
to four,
and if
I, where I is the identity.
As we shall see, the case of
three idempotents can be completely resolved using algebra, indeed
using NCAlgebra. It is known in various cases that if k is equal
to four,
and if
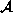 is a Banach algebra, the conclusion is greatly simplified.
This, of course, can not be analyzed using NCAlgebra.
Now we turn to the case of three idempotents and derive the
following theorem.
is a Banach algebra, the conclusion is greatly simplified.
This, of course, can not be analyzed using NCAlgebra.
Now we turn to the case of three idempotents and derive the
following theorem.
Theorem
Let
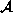 be an algebra and A, B and C be elements
of
be an algebra and A, B and C be elements
of
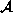 .
If A, B and C are idempotents and
A + B + C =
.
If A, B and C are idempotents and
A + B + C =
 ,
then
,
then
 satisfies a 5th degree polynomial
whose roots are 0, 1, 2, 3 and
³/2.
Furthermore, A, B, and C can be classified, and
A, B and C commute in all cases except
satisfies a 5th degree polynomial
whose roots are 0, 1, 2, 3 and
³/2.
Furthermore, A, B, and C can be classified, and
A, B and C commute in all cases except
 = ³/2.
= ³/2.
Now we turn to proving the theorem and deriving the classification
claimed by the theorem.
The first main step in the proof of the theorem is the following
proposition.
Proposition 1
Let
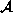 be an algebra and A, B and C be elements
of
be an algebra and A, B and C be elements
of
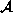 .
If A, B and C are idempotents and
A + B + C =
.
If A, B and C are idempotents and
A + B + C =
 ,
then
,
then
 satisfies a 5th degree polynomial
satisfies a 5th degree polynomial

 -
-

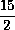

 + 20
+ 20  ³
-
³
-
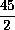

 ²
+ 9
²
+ 9  ,
whose roots are 0, 1, 2, 3 and
³/2.
,
whose roots are 0, 1, 2, 3 and
³/2.
Proof
Let I be the ideal of
K[A,B,C,
 ]
generated by
]
generated by
{A²-A, B²-B, C²-C, A+B+C-
 ,
,
 A - A
A - A
 ,
,
 B - B
B - B
 ,
,
 C - C
C - C
 }
}
The
spreadsheet
shows that
 is a root of a 5th degree polynomial
is a root of a 5th degree polynomial

 -
-

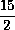

 + 20
+ 20  ³
-
³
-
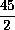

 ²
+ 9
²
+ 9  .
The Solve command in Mathematica shows that the roots
of this polynomial are 0, 1, 2, 3 and
³/2.
.
The Solve command in Mathematica shows that the roots
of this polynomial are 0, 1, 2, 3 and
³/2.
Now we turn to the classification of A, B and C for each of the five
cases, which will show that A, B and C commute in the cases where
lambda does not equal 3/2.
Case  = 0:
Let
= 0:
Let
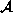 be an algebra. If A, B and C are elements
of
be an algebra. If A, B and C are elements
of
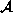 which are idempotents and A + B + C = 0, then
A = 0, B = 0 and C = 0.
which are idempotents and A + B + C = 0, then
A = 0, B = 0 and C = 0.
Proof
See the sum of three idempotents equals zero
problem.
Case  = 1:
There exists an algebra
= 1:
There exists an algebra
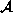 and idempotents a, b and c
of
and idempotents a, b and c
of
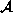 such that a + b + c = 1. Moreover, one can pick
a, b and c to be nonzero.
such that a + b + c = 1. Moreover, one can pick
a, b and c to be nonzero.
Proof
- Example 1:
Let
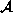 equal the complex numbers and a = 1, b = 0 and
c = 0.
equal the complex numbers and a = 1, b = 0 and
c = 0.
- Example 2: Take
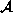 equal to the collection of 3 × 3
matrices over the complex numbers and let
equal to the collection of 3 × 3
matrices over the complex numbers and let
| |
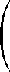
| 1 | 0 | 0 |
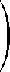
|
| a | = | 0 | 0 | 0
|
| | 0 | 0 | 0
|
| |
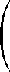
| 0 | 0 | 0 |
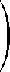
|
| b | = | 0 | 1 | 0
|
| | 0 | 0 | 0
|
| |
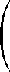
| 0 | 0 | 0 |
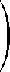
|
| c | = | 0 | 0 | 0
|
| | 0 | 0 | 1
|
- A Gröbner Basis
approach is to consider the ideal
I generated by
{A² - A,
B² - B,
C² - C,
A+B+C-1}.
If we set
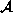 = Q[A,B,C]/I and
a = A + I, b = B + I and c = C + I, then
a, b and c are idempotents which satisfy
a + b + c = 1.
The Gröbner Basis is shown
here.
Note that it is not necessary for A, B,
and C to be zero, but
A and B commute, and their product is zero.
From the given relation
C = 1 - A - B,
we can see that C also commutes with A and B.
Also, C multiplied by either A or B is zero.
= Q[A,B,C]/I and
a = A + I, b = B + I and c = C + I, then
a, b and c are idempotents which satisfy
a + b + c = 1.
The Gröbner Basis is shown
here.
Note that it is not necessary for A, B,
and C to be zero, but
A and B commute, and their product is zero.
From the given relation
C = 1 - A - B,
we can see that C also commutes with A and B.
Also, C multiplied by either A or B is zero.
Case  = 2
There exists an algebra
= 2
There exists an algebra
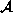 and idempotents a, b and c
of
and idempotents a, b and c
of
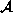 such that a + b + c = 2. Moreover, one can pick
a, b and c to be nonzero.
such that a + b + c = 2. Moreover, one can pick
a, b and c to be nonzero.
Proof
The proof is analogous to the one above where the Gröbner
Basis is
here.
Notice that A and B commute again,
and therefore C commutes with both of them.
Case  = 3
For every algebra
= 3
For every algebra
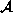 ,
there exists idempotents a, b and c
of
,
there exists idempotents a, b and c
of
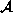 such that a + b + c = 3. Moreover, a, b and
c must be equal to the identity element of
such that a + b + c = 3. Moreover, a, b and
c must be equal to the identity element of
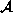 .
.
Proof
The proof is analogous to the one above where the Gröbner
Basis is
here.
Case  =
³/2
For every algebra
=
³/2
For every algebra
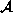 ,
there exists idempotents a, b and c
of
,
there exists idempotents a, b and c
of
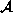 such that a + b + c =
³/2.
such that a + b + c =
³/2.
Proof
The proof is analogous to the one above where the Gröbner
Basis is
here.
In this case, A and B need not commute.
The equation to take note of is
B A + A B - A - B =
³/4.


![]() be an algebra and A, B and C be elements
of
be an algebra and A, B and C be elements
of
![]() .
If A, B and C are idempotents and
A + B + C =
.
If A, B and C are idempotents and
A + B + C =
![]() ,
then
,
then
![]() satisfies a 5th degree polynomial
whose roots are 0, 1, 2, 3 and
³/2.
Furthermore, A, B, and C can be classified, and
A, B and C commute in all cases except
satisfies a 5th degree polynomial
whose roots are 0, 1, 2, 3 and
³/2.
Furthermore, A, B, and C can be classified, and
A, B and C commute in all cases except
![]() = ³/2.
= ³/2.
![]() be an algebra and A, B and C be elements
of
be an algebra and A, B and C be elements
of
![]() .
If A, B and C are idempotents and
A + B + C =
.
If A, B and C are idempotents and
A + B + C =
![]() ,
then
,
then
![]() satisfies a 5th degree polynomial
satisfies a 5th degree polynomial
![]()
![]() -
-
![]()
![]()
![]()
![]() + 20
+ 20 ![]() ³
-
³
-
![]()
![]()
![]() ²
+ 9
²
+ 9 ![]() ,
whose roots are 0, 1, 2, 3 and
³/2.
,
whose roots are 0, 1, 2, 3 and
³/2.
![]() ]
generated by
]
generated by
![]() is a root of a 5th degree polynomial
is a root of a 5th degree polynomial
![]()
![]() -
-
![]()
![]()
![]()
![]() + 20
+ 20 ![]() ³
-
³
-
![]()
![]()
![]() ²
+ 9
²
+ 9 ![]() .
The Solve command in Mathematica shows that the roots
of this polynomial are 0, 1, 2, 3 and
³/2.
.
The Solve command in Mathematica shows that the roots
of this polynomial are 0, 1, 2, 3 and
³/2.