[next] [prev] [prev-tail] [tail] [up]

Chapter 11
Demo on NCGB - Matrix Computation

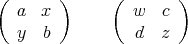
(The functions used in this notebook require the C++ NCGB module.)

11.1 The Partially Prescribed Inverse Problem

This is a type of problem known as a matrix completion problem. This particular one was suggested by Hugo Woerdeman. We are grateful to him for discussions.

Problem: Given matrices a, b, c, and d, we wish to determine under what conditions there exists matrices x, y, z, and w such that the block matrices

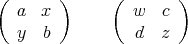
( ) ( ) a x w c y b d z
are inverses of each other. Also, we wish to find formulas for x, y, z, and w.

This problem was solved in a paper by W.W. Barrett, C.R. Johnson, M. E. Lundquist and H. Woerderman [BJLW] where they showed it splits into several cases depending upon which of a, b, c and d are invertible. In our example, we assume that a, b, c and d are invertible and discover the result which they obtain in this case.

First we set all of our variables to be noncommutative and set up the relations which make matrices a, b, c, and d invertible. (Inverses in this particular problem are taken to be two sided.) Strong invertibility relations help when one is trying to get an idea of the solution of the problem.

In[1] := SetNonCommutative[a,b,c,d,w,x,y,z,Inv[a],Inv[b],Inv[c],Inv[d]];

Then we define the relations we are interested in. The two relations oneway, otherway set our block matrices as inverses of each other. The relations inverses invoke the assumption that a,b,c, and d are invertible by defining their inverses.

In[2]:= first  = {{a,x}, {y,b}}  
        second = {{w,c},{d,z}} }  
Out[2] = {{a,x}, {y,b}}  
Out[3] = {{w,c}, {d,z}}  
In[4]:= oneway = MatMult[first,second] - IdentityMatrix[2]  
        otherway = MatMult[second,first] - IdentityMatrix[2]  
Out[4] = {{-1+a**w+x**d,a**c+x**z}, {b**d+y**w,-1+b**z+y**c}}  
Out[5] = {{-1+c**y+w**a,c**b+w**x}, {d**a+z**y,-1+d**x+z**b}}  
In[6]:= inverses = {-1 + a ** Inv[a], -1 + Inv[a] ** a,  
          -1 + b ** Inv[b], -1 + Inv[b] ** b,  
          -1 + c ** Inv[c], -1 + Inv[c] ** c,  
          -1 + d ** Inv[d], -1 + Inv[d] ** d  
        }  
        allRelations = Join[ Flatten[{ oneway, otherway }],  inverses]}  
Out[6] = {-1+a**Inv[a],-1+Inv[a]**a, -1+b**Inv[b],-1+Inv[b]**b,  
         -1+c**Inv[c],-1+Inv[c]**c,-1+d**Inv[d],-1+Inv[d]**d}  
Out[7] = {-1+a**w+x**d,a**c+x**z, b**d+y**w,-1+b**z+y**c,  
         -1+c**y+w**a,c**b+w**x,d**a+z**y,-1+d**x+z**b,  
         -1+a**Inv[a],-1+Inv[a]**a, -1+b**Inv[b],-1+Inv[b]**b,  
         -1+c**Inv[c],-1+Inv[c]**c, -1+d**Inv[d],-1+Inv[d]**d}

Specify to NCAlgebra which variables are known and which are unknown. To GB fans this sets the monomial order indicated around the middle of the first page of the output.

In[8]:= SetKnowns[a, Inv[a], b, Inv[b], c, Inv[c], d, Inv[d]]  
        SetUnknowns[{z}, {x, y, w}]

Tell NCAlgebra to solve for our unknown variables

In[10]:= answer = NCProcess[allRelations, 4, ‘‘DemoGBMA" ];  
> Outputting results to the stream  
> OutputStream[‘‘DemoGBMA.tex", 11]  
> Done outputting results to the stream  
OutputStream[‘‘DemoGBMA.tex", 11]

The TEX output which appears shows that, if a, b, c and d are invertible, then one can find x, y, z and w such that the matrices above are inverses of each other if and only if z b z = z + d a c.

The TEX output also gives formulas for x, y and w in terms of z.

Input = - 1 + aw + xd ac + xz bd + y w - 1 + bz + y c - 1 + cy + w a cb + w x da + z y - 1 + dx + z b - 1 + aa-1 - 1 + a-1 a - 1 + bb-1 - 1 + b-1 b - 1 + cc-1 - 1 + c-1 c - 1 + dd-1 - 1 + d-1 d File Name = DemoGBMA
NCMakeGB Iterations = 4
NCMakeGB on Digested Iterations = 5
SmallBasis Iterations = 5
SmallBasis on Knowns Iterations = 6
Deselect→{}
UserSelect→{}
UserUnknowns→{}
NCShortFormulas→-1
RR→True
RRByCat→False
SB→False
SBByCat→True
DegreeCap→-1
DegreeSumCap→-1
DegreeCapSB→-1
DegreeSumCapSB→-1
NCCV→True
THE ORDER IS NOW THE FOLLOWING: a < a-1 < b < b-1 < c < c-1 < d < d-1 ≪ z ≪ x < y < w __________________________ __________________________  YOUR SESSION HAS DIGESTED ___________________________________ __________________________  THE FOLLOWING RELATIONS ___________________________________ ___________________________________________________________________________________ THE FOLLOWING VARIABLES HAVE BEEN SOLVED FOR: {w, x, y}
The corresponding rules are the following:

w → a-1 d-1 z bd

x → d-1 - d-1 z b

y → c-1 - bz c-1

___________________________________________________________________________________
The expressions with unknown variables {}
and knowns {a, b, c, d, a-1, b-1, c-1, d-1}
aa-1 → 1

bb-1 → 1

cc-1 → 1

dd-1 → 1

a-1 a → 1

b-1 b → 1

c-1 c → 1

d-1 d → 1

___________________________________________________________________________________ _______________________  USER CREATIONS APPEAR BELOW _______________________________ ___________________________________________________________________________________ ___________________________________________________________________________________ ____________________  SOME RELATIONS WHICH APPEAR BELOW ___________________________ ______________________________  MAY BE UNDIGESTED ________________________________________ ___________________________________________________________________________________ THE FOLLOWING VARIABLES HAVE NOT BEEN SOLVED FOR: {a, b, c, d, z, a-1, b-1, c-1, d-1}
___________________________________________________________________________________
1.0 The expressions with unknown variables {z}
and knowns {a, b, c, d}
z bz → z + dac

The time for preliminaries was 0:00:06
The time for NCMakeGB 1 was 0:00:01
The time for Remove Redundant 1 was 0:00:03
The time for the main NCMakeGB was 0:00:21
The time for Remove Redundant 2 was 0:00:09
The time for reducing unknowns was 0:00:03
The time for clean up basis was 0:00:05
The time for SmallBasis was 0:03:44
The time for CreateCategories was 0:00:01
The time for NCCV was 0:00:19
The time for RegularOutput was 0:00:02
The time for everything so far was 0:04:57

[next] [prev] [prev-tail] [front] [up]