Chapter 31
NCXFindChangeOfVariables: The Long Description
The main purpose of NCXFindChangeOfVariables is to take some list of polynomials, probably the result
running NCProcess on some (possibly large) problem and to find a motivated unknown which simplifies
the problem. A motivated unknown M is a polynomial which, when substituted into some polynomial
which motivates it, produces a polynomial in only one unknown, namely M. Furthermore, we want M to
be nontrivial in the sense that given a polynomial P in knowns and unknowns, M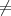 aP + b where a and b
are numbers.
aP + b where a and b
are numbers.
NCXFindChangeOfVariables does not accomplish this, but it often finds solutions. The method is to
find a number of candidates for motivated unknowns and then try them one by one until we find
one which, in fact, works. Trying the candidates involves running a Grobner basis algorithm
(NCProcess) on each possibility. To make things more efficient, there are a number of ways
we may try to eliminate candidates or reorder them so that we find the motivated unknown
faster.
31.1 Details of the Algorithm
31.1.1 Preparation
The first step is to put motUnknown and Tp[motUnknown] in the order. If the variable motUnknown is
already in the order, then nothing is done. Otherwise, the two variables are put in the order in a graded
piece just after the knowns. For example, if the old order is a < b < c ≪ x < xT ≪ y then the new order
would be a < b < c ≪ motUnknown < motUnknownT ≪ x < xT ≪ y.
The default options are also set at this stage.
31.1.2 Collect and extract
The next step is to go through the polynomials and to collect on knowns and on monomials consisting
only of knowns. The NCAlgebra command NCCollectOnVariables looks for knowns and collects
terms around them. For instance, given xyax + zax, NCCollectOnVariables would return
(xy + z)ax. The first set of candidates for motivated unknowns is to extract what is collected
to either side of the known. The program now keeps a list of pairs {P, C} where P is the
polynomial on which NCCollectOnVariables was called and C is one of the things collected
to either side of the knowns. The resulting list has all such pairs related to the given list of
polynomials.
Note that if nothing can be collected, no entries are returned and our algorithm cannot find a
motivated unknown.
31.1.3 Eliminate candidates which are too small
The next step is to look at the number of unknowns in the candidates for motivated unknowns and to try
to eliminate some without running a Grobner basis algorithm. This step counts the number of unknowns
in the candidate (C in the pair described above) and compares it to the number of unknowns in the
polynomial that motivated it (P above). Since the idea is that the candidate C will reduce P to a function
of one variable, we can eliminate the pair if C has less unknowns than P. This is exactly what this step
does.
It also eliminates pairs where C is just one variable.
31.1.4 Eliminate purely numerical terms from candidates - Default is Off
Here we eliminate purely numerical terms from the candidates for motivated unknowns. Thus if our
candidates starts as xy + 1 we instead take as our candidate xy. I’m not sure if this step is still
necessary, but in the past there were difficulties matching when the candidate had a numerical
term.
To turn off this step, redefine NCXKillConstantTerms to be the identity function, i.e.
NCXKillConstantTerms[list_] := list.
31.1.5 Sort list of candidates by number of terms
Now we sort the candidates by their length, where by length we mean the number of terms in the
polynomial. It generally turns out that the smallest polynomials are more likely to work, so by
sorting in such a way that the polynomials with the least number of terms come first, we
will probably find the motivated unknown (if one exists) earlier than if we had a random
order.
31.1.6 Multiply through by monomials - Default is off
Sometimes it turns out that we need to find the motivated unknown, we actually need to multiply the
polynomial P by some monomial on the left and/or right. Then this new polynomial will admit a
motivated unknown. This step adds new pairs {P’, C’} where P’ is a LPR where P is from the original list
and L and R are monomials. L and R are dtermined in the following way. Given a pair {P, C} from the
original list we find all prefixes L of the leading term of C and all suffixes R of the leading term of C.
Prefixes of a monomial M are monomials on the left of M and suffixes are monomials on the right.
Thus the monomial xyz has prefixes x, xy, and xyz and has suffixes z, yz, and xyz. We add
to our list pairs {LP, C}, {PR, C}, and {LPR, C}. These candidate pairs are added at the
end of the list so that they are tried after the candidates without multiplying through by
monomials.
This option needs to be hcanged so that lists can be multiplied through solely on the left
or solely on the right.
In order to turn this on, give the option MultiplyByMonomials -> True.
31.1.7 Run the Grobner basis algorithm
We now can step through out list and try each to see if the candidate is, in fact, a good motivated
unknown. Given a pair {P, C} we run NCProcess on the union of the P, polynomials with 2 terms (these
we shall think of as important polynomials since they include relations defining inverses and
symmetry), and the rules C → motUnknown and CT → motUnknownT . If it finds a motivated
unknown that works (i.e. eliminates all other unknowns), then it stops and returns the pair
{P,C}.
31.1.8 Options
Most of these steps can be eliminated by setting the appropriate option. See manual for details in setting
options.
31.2 Finding Coefficients of Variables in a Polynomial
31.2.1 NCCoefficientList[Expression, aListOfIndeterminants]
-
- Aliases: None
-
- Description: This generalizes the Mathematica command CoefficientList[Expression,
aListOfIndeterminants] to noncommutative algebras. There are many legitimate
generalizations to the noncommuting case and we picked one here.The user can experiment
to see if it is what he wants.
-
- Arguments:
-
- Comments / Limitations:
31.3 Main Change Of Variables Command
The main command is NCXFindChangeOfVariables. The general purpose of these commands is to
produce 1-strategies from a given list of relations. That is, we would like to find a motivated unknown
that eliminates all other unknowns from some equation in a nontrivial way. By nontrivial, we mean that
the motivated unknown is not the entire given expression E or aE + b where a and b are
numbers.
31.3.1 NCXFindChangeOfVariables[ aListofPolynomials, anInteger, aString, Options]
-
- Aliases: None
-
- Description: This command needs the monomial order to already be set. It then uses the ambient
order in NCGB. NCXFindChangeOfVariables[ aListOfPolynomials,
anInteger, aString, Options] takes a list of relations aListOfPolynomials, finds the
candidates for motivated unknowns and then tries each one in NCProcess until it finds that
all unknowns except the candidate have been eliminated (and hence would make a good
motivated unknown). If it finds a motivated unknown (which absorbs all other unknowns)
then it returns a list {E, M} where M is the motivated unknown and E is the expression which
motivated it. Otherwise it returns False. It can also be made to return a list of outputs from
the calls to NCProcess.
-
- Arguments: aListofPolynomials is a list of polynomials, aString is a string for the beginning of the tex
files produced by NCProcess, and anInteger is the number of iterations for NCProcess. The options
are:
- IncludeTranspose → False: This option adds the transpose of the candidate to the set
of relations. The default (False) is not to add the transpose relation, while setting it to
True will not add the transpose relation.
- AllRelations → False: This option determines whether the Grobner Basis is computed
using only the relation that motivated the candidate together with the candidate or if
it uses all of the given relations plus the candidate. The default (False) only uses the
polynomial that motivated the unknown plus all relations of length 2 (these we will
consider “important” relations and include relations defining inverses and symmetry)
while setting it to True uses all of the relations.
- CountV ariables → True: This option determines whether or not
NCXPossibleChangeOfVariables[ ] eliminates the candidates which do not contail all
of the unknowns present in the polynomial that motivated it (and thus the candidate
cannot reduce that polynomial to a polynomial in one variable). The default (True)
does eliminate these possibilities while setting it to False does not do this elimination.
- MultiplyByMonomials → False: This option determines whether or not
NCXMultiplyByMonomials is called, so that if no candidate works, it tries to multiply
though by monomials on the left and/or right. The default (False) does no multiplying,
while setting it to True tries multiplying through by monomials.
- SortByTermLength → True: This option decides whether or not to sort the results
of NCXPossibleChangeOfVariables by the length (number of terms) in the candidate
(shortest to longest). The default (True) does sort it so that it tries the shortest
candidates first (since in practice the longer ones don’t tend to work). Setting it to False
does not do the sorting step.
- NCProcessOptions → {SBByCat → False,RR → False}: This allows one to set
additional options when NCProcess is run. The default is {SBByCat → False,RR →
False}. A typical setting might be NCProcessOptions- > {SBByCat →
False,NCCV → True}. list of the outputs from NCProcess.
- StopIfFound → True: This option determines whether the program stops if a
motivated unknown is found. The default (True) stops if a motivated unknown is found
and returns only this pair. Setting this option to False runs all possibilities in NCProcess
and returns all of the results (whether a motivated unknown is found or not).
-
- Comments / Limitations: This procedure uses the ambient monomial order in NCGB.
Furthermore, the monomial order is changed by this program. The variables motUnknown and
Tp[motUnknown] are inserted in a graded piece between the current knowns and unknowns
if these variables are not already present. This function runs NCProcess many times and
therefore produces a number of tex files (actually, it produces exactly Length[NCXMultiplyBy
Monomials[NCXPossibleChangeOfVariables[aListOfPolynomials, Options]]] tex
files). These files are named nameno# where name is the string given as an argument, no is
added and # is a number. This function uses NCProcess,
NCXPossibleChangeOfVariables, NCXMultiplyByMonomials.
The following command may also be useful since it gives a list of expressions, each of which is a possible
new variable. It runs all steps above except the last two, that is, multiplying through by monomials and
running the Grobner basis.
31.3.2 NCXPossibleChangeOfVariables[ aListofPolynomials, Options]
-
- Aliases: None
-
- Description: NCXPossibleChangeOfVariables[ aListOfPolynomials, Options] takes a list of
relations and looks for a good motivated unknown. It returns a list of pairs {E, M} where
E is the expression which motivated the candidate M and M is the candidate for a motivated
unknown.
-
- Arguments: aListofPolynomials is a list of relations and options can be any of the following:
- CountV ariables → True: The CountVariables option counts to see if the candidate for
motivated unknown has all of the variables in the expression which motivated it, and
removes the entry from the list if it does not (and thus could not reduce the expression
to one unknown). The default (True) is to eliminate these entries, while False will skip
this step entirely.
- RemoveNumbers → False: The RemoveNumbers option decides whether or not to
remove purely numerical terms from the candidates. If True, then these terms are
removed. For instance, the candidate xy + 1 becomes xy. If set to False, the candidate
is not be changed.
- SortByTermLength → True: The SortByTermLength option decides whether or not
to sort the results by the length (number of terms) of the candidate (with the shortest
first). The default (True) does the sorting, while setting the option to False does not
sort at all.
-
- Comments / Limitations: The candidate for motivated unknown is found by first doing an
NCCollectOnVariables[ ], which collects around knowns, on each relation and then looking
at what is found on either side of the knowns. These are the candidates for motivated
unknowns. The next step is to eliminate candidates which do not contain all of the
unknowns present in the expression which motivated them. This option can be turned off by
CountV ariables → False. The next step is to eliminate purely numerical terms from the
candidates (so that you won’t get an expression like xy + 1 for a candidate, but xy instead).
The final step is to sort the pairs by length (number of terms) of the motivated unknown,
the shortest being first. This is done because long candidates usually do not eliminate all of
the variables. This option can be turned off by SortByTermLength → False.
31.4 Less Valuable Change of Variables Commands
These commands are used by the above commands. They would not be of use to the average
user.
31.4.1 NCXMultiplyByMonomials[ aVerySpecialList]
-
- Aliases: None
-
- Description: NCXMultiplyByMonomials[ aVerySpecialList] takes a list like the one returned
by NCXPossibleChangeOfVariables and returns the list appended (possibly) with new pairs
which are multiplied through by certain monomials (prefixes and suffixes of the candidate
for motivated unknown) on the left and/or right.
-
- Arguments: aVerySpecialList is list of pairs of polynomials, so it looks like {{poly1, poly2},
...,{poly3,poly4}} where poly1,..., poly4 are polynomials.
-
- Comments / Limitations: A new pair is gotten from an old pair by looking at the candidate for
motivated unknown and then multiplying by prefixes and suffixes of the candidate.
31.4.2 NCXAllPossibleChangeOfVariables[ aListOfPolynomials]
-
- Aliases: None
-
- Description: NCXAllPossibleChangeOfVariables[ aListOfPolynomials] takes a list of
polynomials and returns a list of pairs {P, C} where P is a polynomial from
aListOfPolynomials and C is on the left or right side of a product of knowns inside P after
P has been collected (with NCCollectOnVariables).
-
- Arguments: aListOfPolynomials is a list of polynomial expressions.
-
- Comments / Limitations: This procedrue uses the ambient order, so it must be set
before use. This procedure returns a dumb set of candidates for motivated unknowns.
NCXPossibleChangeOfVariables uses it and returns a more intelligent list of candidates.
Thus the average user would not find a need for this procedure.
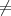 aP + b where a and b
are numbers.
aP + b where a and b
are numbers.
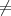 aP + b where a and b
are numbers.
aP + b where a and b
are numbers.