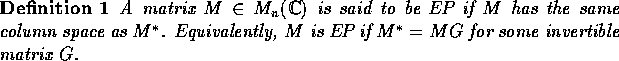
A solution to Problem 26 - 4
in Image April 2001 volume 26; proposed by Yongge Tian ytian@mast.Queensu.CA
Queens University, Kingston Ontario, Canada
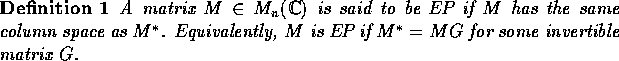
A slight modification of the original Problem 26-4 is
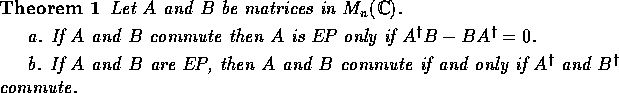
Solution.
The goal is to give a proof based upon fairly automatic use of computer algebra. We use NCGB package of NCAlgebra. Available from http://www.math.ucsd.edu/~ncalg.
(a) Problem 26-4 asked whether, under the condition that A and
B commute, A is EP if and only if
![]() .
Observe that only one implication is always
true, for if B is the identity matrix, then B commutes
with both A and its pseudo-inverse regardless of whether A is EP or not.
.
Observe that only one implication is always
true, for if B is the identity matrix, then B commutes
with both A and its pseudo-inverse regardless of whether A is EP or not.
In the other direction, if A and B commute and A is EP, then we show
that ![]() and B commute using a noncommutative (NC) Gröbner basis
algorithm.
Recall that the input to a Gröbner basis algorithm has two parts.
The first part
is a list
of polynomials, denoted by
and B commute using a noncommutative (NC) Gröbner basis
algorithm.
Recall that the input to a Gröbner basis algorithm has two parts.
The first part
is a list
of polynomials, denoted by ![]() , which
in our solution of this problem is:
, which
in our solution of this problem is:
which when set to zero define the pseudo-inverse of A.
![]()
![]()
The second part of the input is an order on monomials which typically is induced by an order on the variables in the problem. In our case the order is degree lexicographic order induced by the following order on variables:
Recall that in a Gröbner basis algorithm variables which are high in the order tend to be eliminated before variables which are low in the order.
We use the command NCProcess, with options set so that it makes and sorts an NC Gröbner basis by running Mora's algorithm for four iterations and removes some redundant polynomials. This makes a long list of polynomial equations, one of which is Q=0. This shows that part (a) is true. The run took 49 minutes on a 1 GigaHertz Pentium III machine with one gigabyte of RAM.
(b) Suppose A and B commute. Again we use the Gröbner basis package applied to the starting relations:
![]()
![]()
![]()
![]()
is zero.
The converse is obtained similarly. In the input polynomials we merely replace
![]()
by
![]()
and redefine
Q by adjoining the polynomial Q-AB +BA
instead of ![]() ;
we do this since our goal is now to show that
A and B commute.
Again we choose a degree lexicographic order with Q at the top
and find after 3 iterations and about 15 minutes that Q=0. Again
we tried some variations on the orders and in each case found that Q=0.
;
we do this since our goal is now to show that
A and B commute.
Again we choose a degree lexicographic order with Q at the top
and find after 3 iterations and about 15 minutes that Q=0. Again
we tried some variations on the orders and in each case found that Q=0.
This solves problem Problem 26 - 4 by fairly automatic use of NCAlgebra's noncommutative Gröbner basis package and suggests a problem of our own: Now that some noncommutative computer algebra is available, which of the purely algebraic problems ( with a modest number of variables and equations ) that have been posed over the past years in Image succumb to computer algebra?
Submitted to:
werner@united.econ.uni-bonn.de
Hans Joachim Werner,
IMAGE Editor-in-Chief,
Institute for Econometrics and Operations Research,
Econometrics Unit,
University of Bonn,
Adenauerallee 24-42m D-53113
Bonn, Germany
This document (.tex) (.ps) (.pdf).
Here are the files for (a)'s run:
Here are the files for (b)'s run:
Forwards direction:
Backwards direction: