Strategy

The idea of a strategy is the similar to that of a prestrategy, except that it incorporates motivated unknowns. The idea of a strategy is :

The input to a strategy is a set of equations C.

S0 . Set .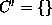

S1 . Run NCProcess1 which creates a display of the output (see O1-O5 in §) which contains collected forms of the polynomial equations. Look at the list of polynomials involving only one unknown or one motivated unknown (say a particular equation 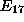only depends upon the motivated unknown ).

S2 . The user must now make a decision about equations in (e.g., 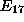is a Ricatti equation so I shall not try to simplify it, but leave it for Matlab). Now the user declares a new unknown y and adds the relation as a user creation. The user would also select the equation 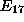as important. User selecting an equation corresponds to adding it to the set 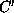. See § for variants on this step.

S3 . Either do the ``End game'' (see §) or Go to S1 .

The above listing is, in fact, a statement of a 1-strategy. Sometimes one needs a 2-strategy in that the key is equations in 1 or 2 unknowns (motivated or not). Typically, if a problem is solved with a 1-strategy, then the computer has done a lot for you, while if the problem requires a 2-strategy, then it has done less, and with a 3-strategy much less.

As with a prestrategy, the point is to isolate and to minimize what the user must do. This is the crux of a strategy.