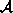-- the algebra might be
n × n
matrices, bounded linear transformations
on a complex separable Hilbert space or a variety of
other algebras
.
This paper concerns
algorithms which assist in transforming the collection
of equations into a more suitable form.
In this paper, we will blur the difference between the polynomial equation p = q and the polynomial p - q. An algebraist would say that p is a relation and an analyst would say that p = 0 is a polynomial equation. The difference in language does not lead to problems.