Solving (HGRAIL) using NCProcess
The first step is to assemble all of the key
polynomial equations in executable form:
The polynomials we shall input to NCProcess1 are
naturally thought of
in several groups.
First, to enforce that the 2 x 2 matrix
(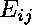 )
i=1, 2, j=1, 2
is symmetric, we require each of the following polynomials to be zero:
)
i=1, 2, j=1, 2
is symmetric, we require each of the following polynomials to be zero:
We also assume that
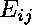 is invertible for i=1, 2
and j=1, 2. We assume the following polynomials are zero:
Naturally we also
assume the following polynomials are zero:
The multigraded lexicographic order
which we use is:
is invertible for i=1, 2
and j=1, 2. We assume the following polynomials are zero:
Naturally we also
assume the following polynomials are zero:
The multigraded lexicographic order
which we use is:
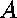

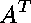

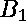

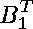

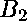

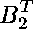

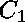

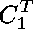

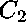

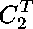

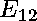

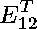

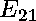

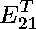



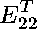



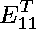

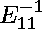

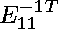





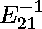

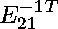

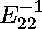

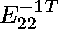

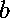

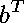



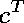

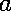

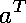
We ran NCProcess1 for 2 iterations
with the option NCCollectOnVariables turned on.
The algorithm did not run the full two iterations but
finished after one.
Our program produced a message saying that, in fact, the output
is a Gröbner Basis (rather than a partial GB).
Step 1 : Process and Collect
There is no point in listing the full
spreadsheet here.
Indeed, the only nontrivial undigested polynomial equations are:
The expressions with unknown variables
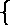
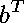

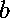






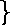
and knowns
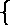


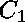

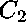

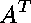

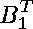

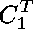

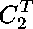
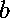
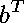

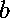
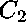



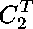
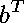



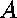




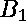
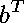


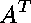




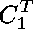
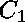


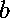



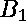
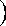
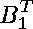


The expressions with unknown variables
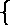
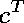











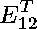

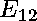
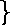
and knowns
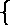
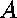

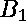

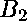

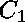

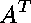

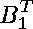

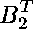

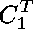
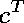


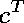
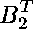
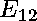









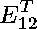
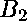




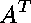
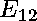




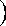



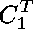
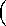


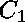


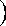

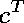
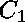



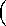




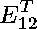







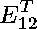
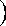
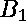
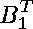
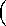
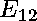




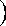
Step 2: The user attacks
Now the reader must apply his expertise to the
nontrivial polynomial equations left undigested by
the NCProcess1 command.
A key observation is that the first key
polynomial equation contains
b but not c and the second key polynomial equation
contains c but not b. In other words,
b and c appear in decoupled equations.
Observe that the first key polynomial from the
above spreadsheet is quadratic in b.
We could complete the square and put the polynomial
in the form
where
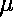 and
and
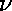 are expressions involving
Since
there are many unknowns in the problem, there is
probably excess freedom.
Let us investigate what happens when we take
are expressions involving
Since
there are many unknowns in the problem, there is
probably excess freedom.
Let us investigate what happens when we take
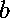

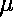

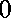 .
This yields the polynomial equation
which we could add to the starting polynomial equations and proceed.
We can also complete the square for the expression in c and
put that expression in the form
We also assume that
.
This yields the polynomial equation
which we could add to the starting polynomial equations and proceed.
We can also complete the square for the expression in c and
put that expression in the form
We also assume that




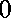 .
This defines c by the following equation
Since we have now
solved for b and c,
we can use these equations to solve for
.
This defines c by the following equation
Since we have now
solved for b and c,
we can use these equations to solve for
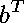 and
and
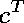 .
.



![]() )
i=1, 2, j=1, 2
is symmetric, we require each of the following polynomials to be zero:
)
i=1, 2, j=1, 2
is symmetric, we require each of the following polynomials to be zero: