[next] [prev] [prev-tail] [tail] [up]

Chapter 2
A More Sophisticated Demo

This demo derives the Bounded Real Lemma for a linear system using NCAlgebra. We will revisit this demo when we introduce NCGB. This is a special case of this lemma for a more general system described in [BHW].

First we load NCAlgebra and do some initialization.

In[1] << NC‘  
In[2] << NCAlgebra‘  
In[3]:= Clear[F, G, A, B, x, W, XX];  
In[4]:= SetNonCommutative[F, G, A, B, C, D, x, W, XX];  
In[5]:= Clear[e, F, G, p];  
In[6]:= e[x_] := tp[x] ** XX ** x  
In[7]:= F[x_, W_] := A ** x + B ** W  
In[8]:= G[x_, W_] := C ** x + D ** W  
In[9]:= tp[XX] = XX;  
In[10]:= p[x_] = tp[Grad[e[x], x]]  
Grad::limited: Grad gives correct answers only for a limited class of functions!  
Out[10]= 2 tp[x] ** XX

PICT

Figure 2.1: System Diagram

These definitions are associated with the system diagram in Figure 2.1, where:

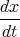dx- dt = F(x,W) = Ax + BW;
out = G(x,W) = Cx + DW.
Now recall definition of Energy Hamiltonian H:
H = outT out - γ2WT W + 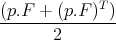(p.F + (p.F)T ) --------------- 2
where
e(x) = xT Xx, p(x) = ∇e(x) = 2(x.X)T

Our goal is to prove the following Lemma:

Lemma 1 Assume (-γ2 + DT D)-1 exists. Then the linear system described above is:

  1. finite gain dissipative with gain bounded by γ2.
  2. the energy function is xT Xx.

if and only if

XX is a positive semi definite solution to the Riccati inequality:

XA + AT X + CT C + (XB + CT D)(γ2 - DT D)-1(BT X + DT C) ≤ 0

Here we do a proof by computation. First compute H:

In[11]:= SetCommutative[gamma];  
In[12]:= H = tp[G[x, W]] ** G[x, W] - ((gammaˆ2)* \  
     tp[W] ** W) + (p[x] ** F[x, W] + tp[F[x, W]] ** tp[p[x]])/2  
Out[12]= (tp[W] ** tp[D] + tp[x] ** tp[C]) ** (C ** x + D ** W) -  
          2  
>    gamma  tp[W] ** W + (2 (tp[W] ** tp[B] + tp[x] ** tp[A]) ** X ** x +  
>       2 tp[x] ** X ** (A ** x + B ** W)) / 2

We perform some initial simplification on H using NCExpand and NCCollect in its symmetric version:

In[13]:= H1 = NCExpand[H]  
                2  
Out[13]= -(gamma  tp[W] ** W) + tp[W] ** tp[B] ** X ** x +  
>    tp[W] ** tp[D] ** C ** x + tp[W] ** tp[D] ** D ** W +  
>    tp[x] ** X ** A ** x + tp[x] ** X ** B ** W + tp[x] ** tp[A] ** X ** x +  
>    tp[x] ** tp[C] ** C ** x + tp[x] ** tp[C] ** D ** W  
In[14]:= H2 = NCCollectSymmetric[H1, {x, W}]  
Out[14]= tp[W] ** (tp[B] ** X + tp[D] ** C) ** x -  
                    2  
>    tp[W] ** (gamma  - tp[D] ** D) ** W +  
>    tp[x] ** (X ** A + tp[A] ** X + tp[C] ** C) ** x +  
>    tp[x] ** (X ** B + tp[C] ** D) ** W

The strategy here is to maximize H and see if it is ≤ 0. First differentiate to find the ”worst” input W. Here we use our limited commmand Grad. We will do much better when we revisit this example using NCGB.

In[15]:= dH = Grad[H2, W]  
Grad::limited: Grad gives correct answers only for a limited class of functions!  
                 2  
Out[15]= -2 gamma  W + 2 tp[B] ** X ** x + 2 tp[D] ** C ** x + 2 tp[D] ** D ** W

We then find the critical W using the even more limited command NCSolve. Again, check out the same problem under NCGB.

In[16]:= Wsol = NCSolve[dH == 0, W]  
NCSolveLinear1::diagnostics:  
         Since the following expression is not zero  
    2 tp[B] ** X ** x + 2 <<1>> + <<3>> + 4 tp[D] ** D ** <<3>> ** x  
          you may want to double check the result.  
          This expression can be retrieved by the command NCSolveCheck[].  
                            2  
Out[16]= {W -> 2 inv[2 gamma  - 2 tp[D] ** D] ** tp[B] ** X ** x +  
                    2  
>      2 inv[2 gamma  - 2 tp[D] ** D] ** tp[D] ** C ** x}

Now plug the critical point back into H using Substitute. Things are getting uglier so we use NCSetOutput to “beautify” Mathematica’s output.

In[17]:= NCSetOutput[All->True]  
In[18]:= Hw1 = Substitute[H2, Wsol]  
          T             T        T  
Out[18]= x  . (X . A + A  . X + C  . C) . x +  
      T             T                   2      T     -1    T  
>    x  . (X . B + C  . D) . (2 (2 gamma  - 2 D  . D)   . B  . X . x +  
                  2      T     -1    T  
>       2 (2 gamma  - 2 D  . D)   . D  . C . x) +  
         T                   2      T     -1  
>    (2 x  . X . B . (2 gamma  - 2 D  . D)   +  
           T    T               2      T     -1      T        T  
>       2 x  . C  . D . (2 gamma  - 2 D  . D)  ) . (B  . X + D  . C) . x +  
         T                   2      T     -1  
>    (2 x  . X . B . (2 gamma  - 2 D  . D)   +  
           T    T               2      T     -1          2    T  
>       2 x  . C  . D . (2 gamma  - 2 D  . D)  ) . (gamma  - D  . D) .  
                  2      T     -1    T  
>     (-2 (2 gamma  - 2 D  . D)   . B  . X . x -  
                  2      T     -1    T  
>       2 (2 gamma  - 2 D  . D)   . D  . C . x)

We now expand the expression using NCExpand

In[19]:= Hw2 = NCExpand[Hw1]  
          T                T    T            T    T  
Out[19]= x  . X . A . x + x  . A  . X . x + x  . C  . C . x +  
        T                   2      T     -1    T  
>    4 x  . X . B . (2 gamma  - 2 D  . D)   . B  . X . x +  
        T                   2      T     -1    T  
>    4 x  . X . B . (2 gamma  - 2 D  . D)   . D  . C . x +  
        T    T               2      T     -1    T  
>    4 x  . C  . D . (2 gamma  - 2 D  . D)   . B  . X . x +  
        T    T               2      T     -1    T  
>    4 x  . C  . D . (2 gamma  - 2 D  . D)   . D  . C . x -  
            2  T                   2      T     -1           2      T     -1  
>    4 gamma  x  . X . B . (2 gamma  - 2 D  . D)   . (2 gamma  - 2 D  . D)   .  
        T                  2  T                   2      T     -1  
>      B  . X . x - 4 gamma  x  . X . B . (2 gamma  - 2 D  . D)   .  
               2      T     -1    T  
>      (2 gamma  - 2 D  . D)   . D  . C . x -  
            2  T    T               2      T     -1           2      T     -1  
>    4 gamma  x  . C  . D . (2 gamma  - 2 D  . D)   . (2 gamma  - 2 D  . D)   .  
        T                  2  T    T               2      T     -1  
>      B  . X . x - 4 gamma  x  . C  . D . (2 gamma  - 2 D  . D)   .  
               2      T     -1    T  
>      (2 gamma  - 2 D  . D)   . D  . C . x +  
        T                   2      T     -1    T  
>    4 x  . X . B . (2 gamma  - 2 D  . D)   . D  . D .  
               2      T     -1    T  
>      (2 gamma  - 2 D  . D)   . B  . X . x +  
        T                   2      T     -1    T  
>    4 x  . X . B . (2 gamma  - 2 D  . D)   . D  . D .  
               2      T     -1    T  
>      (2 gamma  - 2 D  . D)   . D  . C . x +  
        T    T               2      T     -1    T  
>    4 x  . C  . D . (2 gamma  - 2 D  . D)   . D  . D .  
               2      T     -1    T  
>      (2 gamma  - 2 D  . D)   . B  . X . x +  
        T    T               2      T     -1    T  
>    4 x  . C  . D . (2 gamma  - 2 D  . D)   . D  . D .  
               2      T     -1    T  
>      (2 gamma  - 2 D  . D)   . D  . C . x

and try to simplify the expression using NCSimplifyRational

In[20]:= Hw3 = NCSimplifyRational[Hw2]  
                                                                T  
          T                T    T            T    T        D . D  -1  
Out[20]= x  . X . A . x + x  . A  . X . x + x  . C  . (1 - ------)   . C . x +  
                                                                2  
                                                           gamma  
                                 T  
      T            T        D . D  -1  
     x  . X . B . D  . (1 - ------)   . C . x  
                                 2  
                            gamma  
>    ---------------------------------------- +  
                           2  
                      gamma  
                        T  
      T                D  . D -1    T  
     x  . X . B . (1 - ------)   . B  . X . x  
                            2  
                       gamma  
>    ---------------------------------------- +  
                           2  
                      gamma  
                         T  
      T    T            D  . D -1    T  
     x  . C  . D . (1 - ------)   . B  . X . x  
                             2  
                        gamma  
>    -----------------------------------------  
                           2  
                      gamma

and NCCollectSymmetric

In[21]:= Hw4 = NCCollectSymmetric[Hw3, {x}]  
                                               T  
          T             T        T        D . D  -1  
Out[21]= x  . (X . A + A  . X + C  . (1 - ------)   . C +  
                                               2  
                                          gamma  
                     T                                          T  
                    D  . D -1    T                T        D . D  -1  
       X . B . (1 - ------)   . B  . X   X . B . D  . (1 - ------)   . C  
                         2                                      2  
                    gamma                                  gamma  
>      ------------------------------- + ------------------------------- +  
                        2                                 2  
                   gamma                             gamma  
                      T  
        T            D  . D -1    T  
       C  . D . (1 - ------)   . B  . X  
                          2  
                     gamma  
>      --------------------------------) . x  
                         2  
                    gamma

The last output is mathematically equivalent to the well known Riccati inequality, which proves the Theorem, although this may be hard to see in this form. We will further strengthen this claim when we revisit this example using NCGB. Nor for better visualization, we plug in x = 1 and γ2 = 1

In[22]:= Hw5 = Hw4 /. gamma -> 1 /. x -> 1  
                  T        T             T -1  
Out[22]= X . A + A  . X + C  . (1 - D . D )   . C +  
              T             T -1                     T     -1    T  
>    X . B . D  . (1 - D . D )   . C + X . B . (1 - D  . D)   . B  . X +  
      T             T     -1    T  
>    C  . D . (1 - D  . D)   . B  . X

and for extra simplicify set D = 0:

In[23]:= Hw6 = Hw5 /. D -> 0  
                  T        T                T  
Out[23]= X . A + A  . X + C  . C + X . B . B  . X

[next] [prev] [prev-tail] [front] [up]