[next] [prev] [prev-tail] [tail] [up]

Chapter 25
Commands which are not supported

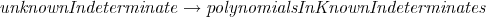
Here we list commands which we started to develop but did not pursue to the point of thorough testing. If we pursue them we may change their calling sequences, etc.

BlockPartition
This probably does not work reliably.
NCEliminate[ExpressionsList,varsList,opts]
This crudely generalizes the Mma command Eliminate to the noncommuting case. You should have set a monomial order before running it. If not, there is an option    UseNewOrder → False   which tells NCEliminate to use its (stupid) default ordering.

25.1 A Mathematica Groebner Basis Package Without C++

The files containing the word Old in their names, many residing in the directory ”OldMmaGB”, contain a primative version of NCGB but all in Mma; no C++. That was our first version.

Probably it still works but we have not tried it in a long time. It is slow, we remember that much. Since there is no document, about the best chance you have at deciphering it is to cruise thru the usage statements and function definitions.

25.2 NCXWholeProcess[ polys, orderList, fileName, grobIters]

This very experimental function makes repeated calls to NCProcess[ ], changing the order at each iteration in an attempt to triangularize the set of relations, polys.

Let us walk through the first iteration of NCXWholeProcess. It begins with the order, orderList, and calls NCProcess[ polys,grobIters,fileName-1 ] creating a LATEXfile, fileName-1.tex.

The output of NCProcess will (hopefully) have polynomials in one unknown. These unknowns will then be regarded as “determined”. These determined unknowns are moved to the bottom of the unknowns in the order.

A polynomial of the form

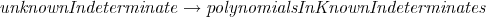
unknownIndeterminate → polynomialsInKnownIndeterminates
is known as a singleton. Determined unknowns associated with singletons are moved to the top of the order and the other determined unknowns are moved to the bottom of the unknowns. That is, the new order is of the form
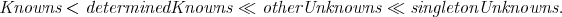
Knowns < determinedKnowns ≪ otherUnknowns ≪ singletonUnknowns.

We have finished the first iteration of NCXWholeProcess. The second iteration goes as follows.

After clearing the old order and setting the new order, NCProcess[ polys,grobIters,“fileName-2”, UserSelects → determinedPolys ] is called creating a file, fileName-2.tex. Here determinedPolys are all polynomials in 0 or 1 unknowns and polys denotes the same set of polynomials that we input in the first iteration. The process is continued, changing the order and calling NCProcess repeatedly.

If no relations in one unknown are discovered at some iteration the currently unknown indeterminates are cyclically permuted. If all cyclic permutations fail to produce any new relations in one unknown the function NCXWholeProcess terminates stating that the problem was not solved. Alternatively, if all unknown variables become determined the function NCXWholeProcess terminates stating that the problem has been solved.

This function is in a very primitive stage and the particulars of it will likely change.

[next] [prev] [prev-tail] [front] [up]