The Bart-Gohberg-Kaashoek-Van Dooren Theorem: Step 3
The End Game
The first step of the end game is to
run NCProcess2 on the last spreadsheet which was produced in
step 2.
The aim of this run of NCProcess2 is to shrink
the spreadsheet as aggressively as possible without
destroying important information. The spreadsheet produced
by NCProcess2 is the same as the last
spreadsheet
which was produced
(It is not hard to see
that NCProcess2 would not have an effect, since the
set of equations found on the previous spreadsheet
can be easily seen to
be minimal. We include the run here for
pedagogical reasons.)
in step 2.
Note that it is necessary that all of the equations
in the spreadsheet have solutions,
since they are implied by the original equations.
The equations involving only knowns play a key role.
In particular, they say precisely that, there must exist
a projection
P
such that
are satisfied.
The converse is also true and can be verified with the assistance
of the above spreadsheet.
To do this, we assume that
the matrices A, B, C and
P
are given
and that the above equations hold, and wish
to define
m ,
m
,
n ,
n ,
a, b, c, e, f and g
such that each of the
equations in the above spreadsheet hold. If we can do this,
then each of the equations from the starting polynomial equations
(FAC) will hold
and we will have shown that
a minimal factorization of
the [A, B, C, 1] system exists.
- Since
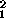P
=
P ,
it is easy to show that there
exists (not necessarily square) matrices
m
and
n
such that
n
m
= 1 and
m
n
=
P.
These are exactly the equations in the
{n1,m1}-Category
of the above spreadsheet.
- Since (1 -
P)²
= 1 -
P ,
it is easy to show that there
exists (not necessarily square) matrices
m
and
n
such that
n
m
= 1 and
m
n
= 1 -
P.
These are exactly the equations in the
{n2,m2}-Category
of the above spreadsheet.
- Since we have defined
m ,
m ,
n
and
n ,
we can define a, b,
c, e, f and g by setting
| a =
n
A
m ,
|
|---|
| b =
n
B,
|
|---|
| c =
C
m ,
|
|---|
| e =
n
A
m ,
|
|---|
| f =
n
B
|
|---|
| and g =
C
m.
|
|---|
These are exactly the equations in the
singleton category.
Here we have used the fact that we are working with
matrices and not elements of an abstract algebra.
With the assignments made above, every equation in the spreadsheet
above holds.
Thus, by backsolving through the spreadsheet,
we have constructed the factors of the
original system [A,B,C,1].
This proves
Theorem ([BGKvD]):
The system [A, B, C, 1] can be factored if and only if
there exists a projection
P
such that
Note that the known equations can be neatly expressed in terms of
P
and
P
= 1 -
P.
Indeed, it is easy to check with a little algebra that these are
equivalent to the
answer we were looking for.
It is a question of taste, not algebra,
as to which form one chooses.
Concluding remarks
The brevity of this presentation in a journal
suppresses some of the advantages and some of the difficulties.
For example, one might not instantly have all
of the insight which leads to the second spreadsheet.
In practice, a session in which someone
``discovers'' this theorem might use many spreadsheets.
All that matters is that one makes a little bit of
progress with each step. Also, since this paper discusses
mathematics and does not explain how to use the code, it is not
easy to see that there is very little which needs to be typed
and that the computer computations are fast.
